This is the worked solution to Challenge Question 1.
To begin thinking about the problem it is a must to visualise or draw out what is actually going on and begin labelling what we know.
As all that matters in this question is the ratio from side to side we can say that the largest square has a side length of 1, the next is 1/2, the next 1/4, etc. This means that the area of the first square is 1, then next is 1/4, the next 1/16, etc.
You can see that there is a ratio of 1/4 between the area of a square and the square before it. So to find the total area of all the squares you can use the formula for the sum of an infinite geometric series a/(1 - r) (explained here), multiply it by 4 (for each branch) and then add 1 (for the central square). So we get [4 × 0.25/(1 - 0.25)] + 1, which gives a total area for the squares as 7/3.
Now for the area of the shaded squares. The first shaded square has a side length of 1/4, so it has an area of 1/16, the next shaded square has a side length of 1/8 and an area of 1/64. You can see that the ratio from the area of one square to the next is 1/16. The total area of the shaded squares uses the sum of an infinite geometric series again and multiplies it by 4 (for each branch). So we get 4 × 0.125/(1 - 1/16), which equals 8/15.
So the area of all the overlapping squares is 8/15 and the total area of all the squares is 7/3, so the proportion of the shaded squares is 8/15 ÷ 7/3 = 0.22857142857... So the final answer is that the shaded squares occupy 22.86% of the total area of the squares.
Sunday 10 June 2012
Challenge Question 1: Solutions
Labels:
challenging maths,
competition,
eBook,
fractals,
fun,
maths,
prize,
question,
squares
Friday 8 June 2012
SOLVED: Challenge Question 2
If you are the first to solve this problem I will give you complete set of the Richard Feynman Lectures on Physics (read up upon the Feynman Lectures on Physics).
Question:
A man, who is 1.65m tall, wishes to find the height of a tree with a shadow 36.52m long. He walks 24.12m from the base of the tree along the shadow of the tree until his head is in a position where the tip of his shadow exactly overlaps the end of the tree top's shadow. How tall is the tree? Round to the nearest hundredth.
Leave answers either in the comments box or contact me with the answer through our contact page or email me at rouge.ray@gmail.com.
Question:
A man, who is 1.65m tall, wishes to find the height of a tree with a shadow 36.52m long. He walks 24.12m from the base of the tree along the shadow of the tree until his head is in a position where the tip of his shadow exactly overlaps the end of the tree top's shadow. How tall is the tree? Round to the nearest hundredth.
Leave answers either in the comments box or contact me with the answer through our contact page or email me at rouge.ray@gmail.com.
Labels:
challenging maths,
competition,
eBook,
Feynman,
fun,
maths,
nature,
prize,
question,
trees
Thursday 7 June 2012
AQA C2 2012 Unofficial Worked Answers
A lot of people found this paper very difficult as some of the questions required more thought than usual. I didn't actually sit this paper, so I couldn't wait to get the paper to see why people found it so difficult. I managed to get hold of the paper so I thought I would share my answers.
You may wish to first download the June C2 2012 paper.

You may wish to first download the June C2 2012 paper.
a.) d = 9
b.) U100 = 23 + 99(9)
U100 = 914
c.) Sn = 0.5n[2a + (n-1)d]
S280 = 140[2(23) + 279(9)]
S280 = 357,980
a.) Area = 0.5 × 26 × 31.5 × 5/13
Area = 157.5cm2
b.) cos(sin-1(5/13))
12/13
c.) AC2 = 262 + 31.52 - (2 × 26 × 31.5 × 12/13)
AC2 = 156.25
AC = 12.5cm
a.) x3 - 2x3/2 + 1
b.) 0.25x4 - 0.8x5/2 + x + c
c.) (0.25(4)4 - 0.8(4)5/2 + 4) - (0.25(1)4 - 0.8(1)5/2 + (1))
42.4 - 0.45
41.95
a.) U1 = 12
U2 = 3
b.) r = 0.25
c.) S∞ = a/(1-r)
S∞ = 12/(1-0.25)
S∞ = 16
d.) U4 = 48(0.25)4 = 0.1875
S∞ = 0.1875/(1-0.25)
S∞ = 0.25

a.) rθ = 18(2π/3)
rθ = 12π
rθ = 12π
b.) i.) α = 2(π - π/3 - π/2)
α = π/3
ii.) PT = QT = 18tan(π/3) = 18√3
Area of two triangles = 2 × 0.5 × 18 × 18√3 = 324√3
Area of sector = 0.5 × 182 × 2π/3 = 108π
Shaded area = 324√3 - 108π = 221.8924551m2
Shaded area = 222m2 to 3 significant figures
a.) i.) f'(2) = 3(2)2 - 4/22 - 11
12 - 1 - 11 = 0
ii.) f''(x) = 6x + 8x-3
f''(2) = 6(2) + 8(2)-3
f''(2) = 13
iii.) f''(x) > 0, so it is a minimum point
b.) y = x3 + 4x-1 -11x + c
1 = 23 + 4(2)-1 -11(2) + c
1 = 8 + 2 - 22 + c
c = 13, so the equation is:
y = x3 + 4x-1 -11x + 13
a.) tanθ + 1 = 0 or sin2θ - 3cos2θ = 0
tanθ = -1
sin2θ = 3cos2θ, divide through by cos2θ to get:
tan2θ = 3
tanθ = ±√3
tanθ = -√3, -1, √3
b.) θ = -45°, 135°, -60°, 120°, 60°
θ = 60°, 120°, 135°
a.) It must go through (0,1)
b.) i.) 7x = 72x - 12
Let a = 7x
a = a2 - 12
a2 - a - 12 = 0
(a - 4)(a + 3) = 0
7x = 4 or 7x = -3; this is illogical so they meet at y = 4
ii.) 7x = 4
log7x = log4
xlog7 = log4
x = log4/log7
x = 0.712 to three significant figures
a.) h = 0.25
x = 0, y = 0; x = 0.25, y = 0.0263; x = 0.5, y = 0.0969; x = 0.75, y = 0.1938; x = 1, y = 0.3010
0.25 × 0.5[(0 + 0.3010) + 2(0.0263 + 0.0969 + 0.1938)]
= 0.117 to 3 significant figures
c.) i.) log1010 + log10x2
log1010 + 2log10x
1 + 2log10x
ii.) 1 + 2log10x = log10(10x2) = log10(√10x)2 = 2log10(√10x)
Stretch parallel to the x-axis scale factor of 1/√10
iii.) 1 + 2log10x = log10(x2 + 1)
log10(10x2) = log10(x2 + 1)
10x2 = x2 + 1
x2 = 1/9
x = 1/3 as x > 0
mOP = log10(10(1/3)2) ÷ 1/3
mOP = 3log10(10/9)
mOP = log10(1000/729)
Labels:
A-Level,
AQA,
AQA C2 2012,
as maths,
core 2,
mark scheme,
maths,
worked answers
Monday 4 June 2012
Deriving the Quadratic Formula
If you have studied Maths up to GCSE level then it is likely that you will have encountered a method of solving any quadratic equation (an equation of the form ax² + bx + c = 0) using the quadratic formula.
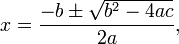
This formula is used to find where the quadratic equation crosses the x-axis (this is at y = 0). Although you have encountered this formula at GCSE it is unlikely that you will have encountered the proof as to why the formula works, which is a shame as it ties in some other GCSE Maths nicely and is in no way complex.
To solve ax² + bx + c = 0 for x you begin by completing the square, rearrange and find what x equals, simple!

And there it is, the quadratic formula! As you can see, it really isn't very difficult to derive the formula and it is a great shame that teachers do not take to the time to show students why the formula works rather than just letting them blindly accept it.
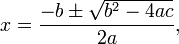
This formula is used to find where the quadratic equation crosses the x-axis (this is at y = 0). Although you have encountered this formula at GCSE it is unlikely that you will have encountered the proof as to why the formula works, which is a shame as it ties in some other GCSE Maths nicely and is in no way complex.
To solve ax² + bx + c = 0 for x you begin by completing the square, rearrange and find what x equals, simple!

Saturday 2 June 2012
Do You Exist?
This may seem somewhat ludicrous to even consider that you may not exist. I mean, you do things, you interact with people, you feel things so obviously you exist, right? Well, not necessarily...
The problem with proving whether or not you exist is that it is very hard to even pin down what existence actually is. It is defined in the dictionary as "objective reality or being", but that poses yet more questions; if we do not know what existence is how can we begin to comprehend reality?
Within mathematics in order to prove something you must only use something that is an already proved axiom. Multiplication works because it is essentially multiple additions (2 × 3 is the same as 2 + 2 + 2). And in fact addition can be proved to be true using something simpler, something more fundamental than itself; logic. You can prove that one plus one equals two (or if you prefer a well explained video), and from this simple fact all other vastly complex mathematics can be used and proved in the knowledge that it is correct.
But existence can not be tackled in the same manner, it is the most fundamental property. Existence precedes even the most basic mathematical principles. We must exist for anything to hold true, including maths. It has to be taken as a given for our principles of logic, maths, science, everything to be true. But this does not prove that we exist. Unfortunately everything else functioning so well because of one assumption does not prove the assumption, it could just be that everything else is radically wrong.
And the main problem of trying to understand our existence - you cannot attack it with maths. You cannot break existence down into a mathematical problem so ones perception of what does, or does not constitute existence is merely subjective. When opinions are the dominant factors of an argument you can never reach a correct answer because essentially, there is none.
I can feel the philosophers amongst you grinding at your teeth, beginning to pound at your keyboard reciting Descartes quote as if it were the ultimate truth. For those of you who do not know of Descartes, he also pondered whether or not he existed but then saw that if he was able to actually ponder his existence then there must on some level be something that exists to do the pondering; hence his quote "I think, therefore I am". It is a well constructed argument, it concisely answers the question using a very logical approach. But that in itself is it's downfall, it uses logic. Logic is something that can only function as a tool if in fact there is existence on some level, so actually he uses the fact that we exist to prove that we exist.
Also, why does the property of thinking create existence? This plays on the difficulty on defining what existence actually is. It almost defines existence as thinking, then citing the fact that we do think to be a proof of existence, which is fundamentally wrong.
So, do you exist? Probably. There is no real means of actually answering the question when we cannot truly define existence. But if you do not exist and your whole life and world is not truly there, you are none the wiser and will never truly know, so why does it matter? Ignorance is bliss as they say. If you wish to believe that you exist, then you exist.
The problem with proving whether or not you exist is that it is very hard to even pin down what existence actually is. It is defined in the dictionary as "objective reality or being", but that poses yet more questions; if we do not know what existence is how can we begin to comprehend reality?
Within mathematics in order to prove something you must only use something that is an already proved axiom. Multiplication works because it is essentially multiple additions (2 × 3 is the same as 2 + 2 + 2). And in fact addition can be proved to be true using something simpler, something more fundamental than itself; logic. You can prove that one plus one equals two (or if you prefer a well explained video), and from this simple fact all other vastly complex mathematics can be used and proved in the knowledge that it is correct.
But existence can not be tackled in the same manner, it is the most fundamental property. Existence precedes even the most basic mathematical principles. We must exist for anything to hold true, including maths. It has to be taken as a given for our principles of logic, maths, science, everything to be true. But this does not prove that we exist. Unfortunately everything else functioning so well because of one assumption does not prove the assumption, it could just be that everything else is radically wrong.
And the main problem of trying to understand our existence - you cannot attack it with maths. You cannot break existence down into a mathematical problem so ones perception of what does, or does not constitute existence is merely subjective. When opinions are the dominant factors of an argument you can never reach a correct answer because essentially, there is none.
I can feel the philosophers amongst you grinding at your teeth, beginning to pound at your keyboard reciting Descartes quote as if it were the ultimate truth. For those of you who do not know of Descartes, he also pondered whether or not he existed but then saw that if he was able to actually ponder his existence then there must on some level be something that exists to do the pondering; hence his quote "I think, therefore I am". It is a well constructed argument, it concisely answers the question using a very logical approach. But that in itself is it's downfall, it uses logic. Logic is something that can only function as a tool if in fact there is existence on some level, so actually he uses the fact that we exist to prove that we exist.
Also, why does the property of thinking create existence? This plays on the difficulty on defining what existence actually is. It almost defines existence as thinking, then citing the fact that we do think to be a proof of existence, which is fundamentally wrong.
So, do you exist? Probably. There is no real means of actually answering the question when we cannot truly define existence. But if you do not exist and your whole life and world is not truly there, you are none the wiser and will never truly know, so why does it matter? Ignorance is bliss as they say. If you wish to believe that you exist, then you exist.
Labels:
cogito ergo sum,
Descartes,
existence,
Gödel,
logic,
mathematics,
philosophy,
proof,
university maths
Subscribe to:
Posts (Atom)












