AS Maths Core 1: Polynomials

Poly, as you may or may not know, means many, and nomial as you likely will not know means terms. Put this together and we get many terms, and that really is the definition of a polynomial. This topic is reasonably large, but none of it is too difficult and it is easy marks to gain in the exam as long as you are careful and know your stuff!

Quadratic Equations

Discriminant
The discriminant of a quadratic equation is something that can tell you how many real roots a quadratic equation will have. If we look at the quadratic equation we know that that you can only find the square root of a positive integer (and zero). The discriminant is what is being square rooted in the quadratic equation (b²-4ac).

If the discriminant is greater than 0 then the quadratic would have two distinct real roots (it crosses the x-axis twice), if the discriminant is equal to 0 then there is one repeated real root (it just touches the x-axis once, at its vertex) and if the discriminant is less than 0 then there are no real roots (it will not touch the x-axis).


If b²-4ac > 0 then the quadratic has two distinct real roots.

If b²-4ac = 0 then the quadratic has one repeated real root.

If b²-4ac < 0 then the quadratic has no real roots.

Quadratic Inequalities
Now, quadratic inequalities can be pretty tricky if you never spent enough time learning them, but if you do spend enough time doing you will be able to get full marks on them every time. First of all the general form of a quadratic inequality is: ax²+bx+c > 0 or ax²+bx+c < 0, note that the signs could also be ≥ or ≤, but this makes no difference in the method but you just need to ensure you use the correct sign in your final answer.

The first thing you need to do is solve the equation equal to zero to get the points that the quadratic crosses the x-axis. Once you have this you need to sketch the quadratic and the shade the side of the quadratic where it is either <0 or 0<. If the quadratic has the sign like this:  ax²+bx+c > 0, you will need to shade only about the x-axis (as that is where y>0), if the inequality is the other way,  ax²+bx+c < 0, then you need to shade below the x-axis (as that is where y<0). It is then easy to see what values the inequality will satisfy.

Example:
Find the range of values that satisfy the inequality,  x²+6x+8 < 0
We’ll begin by solving the equation equal to 0.x²+6x+8, this is then factorised to (x+2)(x+4) = 0, so the quadratic crosses the x-axis at (-2,0) and (-4,0).
Plotting this graph and then shading where the graph is less than 0.

This then means that the inequalities range of results is when x>-4 and x<-2, this can be wrote as a continuous set of values, -4<x<-2.

Note that if the inequality is of the form ax²+bx+c < 0, it will always be a continuous set of values. If it is of the form ax²+bx+c > 0, it will not be a continuous set of values, ever.


Complete the Square
This method of solving quadratics is itself not exactly too efficient and if the quadratic is an awkward one it is often much simpler to use the quadratic formula (which was derived from completing the square) to solve it. But it does have other very useful properties, most of which you will be required to learn.

I will begin by talking you through the steps of how you complete the square of anything.
ax²+bx+c = 0
If we divide the expression through by ‘a’ we get:
x²+(b/a)x+(c/a) = 0
Now if we want to get a perfect square (hence complete the square) we must half the second term, square it, add it on and take it away:
x²+(b/a)x+(b/2a)²-(b/2a)²+(c/a) = 0
Which we can then simplify into the following form:
(x+(b/2a))²-(b/2a)²+(c/a) = 0

Now if you are observant you will see that what is in the bracket with the x is the original number we halved. This will always be the case. Also you should note that -(b/2a)²+(c/a) will be combined as they will both be real numbers.

Now we have our general form of a quadratic in a completed square form, (x+(b/2a))²-(b/2a)²+(c/a) = 0, what can we actually do with it? We can use it to find the vertex of a quadratic equation, going from our example the vertex would be (-(b/2a), -(b/2a)²+(c/a)) . Now this looks pretty confusing but when you apply it to an actual equation it is incredibly easy.

Example:
Find the vertex of 2x²+8x+4=0.
We begin by dividing through by 2 to get, x²+4x+2=0
Halving 4 gives us 2, so our new equation must be:
(x+2)² - 2² + 2 = 0
And on simplifying we get: (x+2)² - 2 = 0
So the vertex must be at (-2, -2)

And it is as easy as that! The only other thing you must know for completing the square is how you change x² into x²+bx+c, and this really is just an extension of completing the square. The vertex of x² is (0,0), so if the vertex of a quadratic is say, (a, b) then the graph of x² is TRANSLATED by 


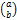
Using our worked example again:
Find the transformation that maps 2x² onto 2x²+8x+4=0

Using our vertex from the previous example, (-2,-2)
This means that x² is translated by 

Remainder Theorem
This again, is very, very easy to do. You just have to watch out for very small errors when doing your calculations and that you do not make an error straight away. To check the remainder when f(x) is divided by (x+a) we get the notation of f(-a), so wherever there is an x in the expression we put a ‘-a’. Whatever this then equals to is the remainder when f(x) is divided by (x+a). This really is all there is to it.

Example:
Find the remainder when f(x) = x³+3x²-6x+4 is divided by (x+2).
f(-2) = (-2)³+3(-2)²-6(-2)+4
f(-2) = -8+12+12+4
f(-2) = 20
Therefore when x³+3x²-6x+4 is divided by (x+2) the remainder is 20.

Factor Theorem
The Factor Theorem is just a special case of the remainder theorem; this is when the remainder of that is equal to 0. For example 6/2 has a remainder of 0 therefore 2 is a factor of 6 (obviously). So (x+a) is a factor of f(x) when f(-a) = 0.

Example:

Verify that (x+2) is a factor of f(x) = x³+4x²+x-6.
f(-2) = (-2)³+4(-2)²+(-2)-6
f(-2) = -8+16-2-6 = 0
f(-2) = 0, therefore (x+2) is a factor of f(x)

Algebraic Long Division
Often you will have one factor of a cubic equation and need to find the other factors. Now there are other ways to do this (factor theorem, solving by inspection, etc.) but personally I find that algebraic long division is the most efficient and accurate way of finding the other factors.

You will only be dealing with factors of the form (x+a), it will never be (2x+a), etc. So it never gets too complicated. I will explain what you need to do with an example.

Now, this is something that might be quite hard to get your head around at first, and you really need to just practice as much as you can. You also need to know that often the quadratic formed can be further factorised. This is true in our example, so representing x³-2x²-5x+6 as a product of three linear factors is: (x+2)(x-1)(x-3). If you have an equation where there is no say 'x' term or 'x²' term you must when dividing it make it 0x² or 0x.

Sketching Graphs

Often you will be required to sketch the graph of a quadratic or a cubic once you have found the roots of the polynomial. There are a few things you have to make sure you do, if you do them you will always get the marks for the quadratic.

• Always mark the points where the polynomial crosses the x-axis and the y-axis.
•  Draw the axes with a ruler.
• Draw the polynomial smoothly; do not draw it bit by bit.
• If you need to draw a line on the graph as well, mark all points of intersection (with graph and axes).
• Make sure you use a pencil in case of mistakes.
• Draw the graph a reasonable size, (I’d go for at least a third of a page if not more).
• Make sure that the shape is roughly correct and resembles the correct polynomial.
• Get the minimum point in roughly the right area.

My advice would be roughly work out where each point is going to be, draw it with a fluid action and then mark the points of intersection on.

And that is it for my guide on polynomials in Core 1, I have taken this from my upcoming eBook revision guide for Core 1, the eBook will also include questions, answers and far more detail. Keep checking back for more.

Euler's Formula

As I mentioned in my previous post on imaginary exponents (read that here), I would explain why in fact Euler's beautiful and immense formula actually works. First of all, I'll actually say what the formula is:
e^ix = Cos(x)+iSin(x)

But this is not exactly intuitive why this is the case. The answer lies in a brilliant piece of maths devised by Brook Taylor, it is called the Taylor series. You can represent any function as the sum of an infinite series of polynomials. This is incredibly useful when it comes to Sin(x), Cos(x) and e^x, and when you delve into the Taylor series of these you can begin to see where e^ix = Cos(x)+iSin(x) comes from:

Now, it might not be immediately obvious how those are related, but all the right terms are there we just need to piece it together. If we begin to manipulate the Taylor series for e^x and we replace 'x' with 'ix' we will begin to see our proof. For the purposes of this I must mention how i^x works i¹ = i, i² = -1, i³ = -i, i⁴ = 1, i⁵ = i,... and it continues in this fashion for all integer powers of i.

Now we have that e^ix = (1 - x^2/2!+ x^4/4!- ((x^6)/6!)+ ...) + i (x - x^3/3!+ (x^5/5!)- x^7/7!+ ...), and these look awfully familiar. In fact if I refer you back to the Taylor series' of Cos(x) and Sin(x):

You can see that these are apparent in what we have now discovered  e^ix to equal. This then means that:

And hence we have our proof of Euler's formula and that e^ix = Cos(x)+iSin(x).
You may have also seen Euler's formula in action as Euler's identity which is often described as the most beautifully profound equation in maths. Euler's identity is e^iπ + 1 = 0, and it is so beautiful because it incorporates the five most important numbers in maths: π, e, 1, 0 and i.

Why does e^iπ + 1 = 0? Well if we look at our proof of Euler's formula, e^ix = Cos(x)+iSin(x) and we input π we get: e^iπ = Cos(π)+iSin(π). Sin(π) = 0, Cos(π) = -1. Therefore  e^iπ = -1, so  e^iπ + 1 = 0.

Imaginary Exponents: x^i

To learn how we do this I first need to explain a very, very useful mathematical formula. It is called "Euler's formula", and this formula gives us a way to find the value of the imaginary exponential function (e^ix) using methods that we already have well defined and are easy to deal with. Euler's formula is: e^ix = Cos(x)+iSin(x), where x is an angle in radians. I may do a post on the actual maths behind why this is the case, but for the purpose of this post it has no relevance.


Now, we can find e^ix, but what use is this if we want to find 2^i, i^i or just anything raised to the power of i, let's call this a^i. So, we want to find a^x where x = i, so we need to try and remember a^x as something involving e raised to the power of something. So this means we have, a^x = e^y.

This then means that a^x = e^[xln(a)]. So we now have a^x in a form involving e raised to a power. So now we can input when x = i. Now by simply placing this into the equation we get, a^i = e^[i*ln(a)]. We can then turn this into something we can solve using Euler's formula, e^[i*ln(a)] = Cos[ln(a)]+iSin[ln(a)].

So now to actually input some numbers to this. Let's say I want to find 2^i, so from our previously defined formula we now have that: e^[i*ln(2)] = Cos[ln(2)]+iSin[ln(2)]. Using our calculators we will find that this is roughly Cos(0.693147)+iSin(0.693147), which then equates to roughly 0.76924+0.63896i. So 2^i ≈ 0.76924+0.63896i

As you can see, this is a complex number and it will be a lot of the time when we deal with imaginary exponents, but (as you may have thought) there are times when the solution to a^i will be a real answer. This is when iSin(x) = 0, and this will happen at Sin(x) = 0 and if you know your Sine curves you will know that this is at Sin(kπ), where k is any integer. Using our formula derived from Euler's, e^[i*ln(a)] = Cos[ln(a)]+iSin[ln(a)], we can see that if a^i is a real number, ln(a) = kπ. If we make both sides to the power of e, we can clear our logarithm to get: a = e^kπ. This should also then mean that the solution that is real (where a = e^kπ) should be equivalent to Cos(kπ).

Therefore if this is correct, then (e^3π)^i should produce a real value. (e^3π)^i = Cos[ln(e^3π)]+iSin[ln(e^3π)]. And when you do work this out, low and behold you get the answer of -1 (which incidentally is the same as Cos(3π)).

Maths and the Real World: Bayes' Theorem

Bayes' Theorem is one of the most practical theorems to apply to everyday life and if used correctly it can be an indispensable decision making tool. In a nutshell what the Bayes' Theorem does is measure the confidence that something is true. It takes the uncertainty before and after observing the modelled system and links the two.


We shall use an example to help explain what the Bayes' Theorem is and how it works. Let's consider the example that you have had a persistent headache for a week now and you're not certain what the cause it. But you do believe that it is caused either by stress (hypothesis A) or by having caffeine (hypothesis B).


So to test if stress is the key to the chronic headaches you have a day of relaxation whilst you've got a headache and have had coffee on the same day. By the end your headache has gone, so this can be considered as evidence. This should have some relation to how much more likely is A than B. But how strong is this evidence exactly? And how do we show which hypothesis it supports? Bayes' Theorem tells us that these answers lie in what is called the Bayes' Factor.


The Bayes' Factor is the question: "How much more likely would it be for this evidence to occur if A were true than if B were true?". This question must lead to one of three conclusions:

1. The evidence would be more likely to occur if A were true than if B were true. This means that the evidence supports A rather than B.
2. The evidence would be just as likely to occur if A or B were true. This means that the evidence has no real weight to whether A or B is more likely to be correct. That means that the "evidence" is not actually evidence at all.
3. The evidence would be more likely to occur if B were true than if A were true. This means that the evidence supports B rather than A.

In our example of chronic headaches the Bayes' factor becomes: "How much more likely would it be for the headache to disappear after having a day of relaxation if stress were the cause compared to if caffeine was the cause?".


Now we do do not know the precise answer to this, but we can give a rough approximation to it. A day of relaxation could have some effect at stopping a headache if caffeine was the cause, but it shouldn't have too much of an effect, no more than a 1 in 5 chance for a persistent headache. On the other hand if the factor of stress is dealt with and the headache disappears, that is a pretty good indication that stress is the key cause, so the chances that stress is the main cause is about 1 in 2.


How likely the headache would have stopped given A is 1/2. How likely the headache would have stopped given B is 1/5. Hence the Bayes' factor, how likely would it be for the headache to stop given A compared to how likely it was to stop given B, is at least (1/2) / (1/5) = 2.5.


This means that given our evidence we should now believe that A is at least 2.5 times more likely compared to B, this is compared to what we used to think. The Bayes' factor tells us how much more our new evidence should cause us to believe the likelihood of one of our hypotheses.


Now let's suppose that you already suspected that stress was twice as likely to be the main cause (as you had recently taken on more responsibility causing more stress). Now we know that the Bayes' Factor is at that A is at least 2.5 times more likely than B, but as we already believe A to be twice as likely as B we know that A is now at least 5 times more likely than B.


Bayes' Theorem is useful because it tells us the correct sort of question to ask ourselves and then it uses maths and statistics to provide us with a suitable answer and easy to understand conclusion. Bayes' Theorem can also provide an answer when looking at just one variable, you simply change B to to A' (not A).


However as humans we tend to have a very poor ability at distinguishing what is or isn't evidence. If we're expecting a particular result we're far more likely to apply whatever evidence we've got and assess it with bias.


So the important part of interpreting the evidence we now have is to always use the question "How much more likely would it be for this evidence to occur if A were true than if B were true?". In the next post I do I will be writing about the maths behind Bayes' theorem.

Estimating Detectable Alien Life: Drake Equation

To begin thinking about what equation we would need to construct to show the number of potentially detectable alien civilizations we must first begin by considering the factors that will affect this number.


Before I begin explaining how we go about constructing the equation I want to first say that this equation is a slightly altered version of the Drake equation, it will yield the exact same results (comment for an explanation as to why) but I personally feel this version is more intuitive and far easier to grasp as a concept. I also need to say that although this is an equation of sorts, it does not have an implicit use that will give a correct answer, the reason for this is just we do not know enough about a lot of the variables to make them constants, so they will change depending on each interpretation.


Well let's start by thinking about what we need as the variables in the equation. The obvious first thing to consider is the number of star systems in our galaxy, we will denote this S. Now our best estimate for this is anything from 200 billion to 600 billion stars, with the increase in the power of our telescopes we get more and more accurate estimates constantly.


A lot of these star systems are simply devoid of any planets at all, they are just a star with no planets at all. So the next variable that we need to consider is the fraction of stars with planets, we will denote this as P. Now this really is a pretty massive estimate, we could never know the exact fraction of stars that have planets, but again we do have methods of checking if a star has a planet and currently it is thought that around 50% of stars have planets too.


Now we currently will have an approximation of the number of stars with planets orbiting them, the next thing we will want to do to narrow down this number to the number of detectable alien life is for what fraction of these star systems lies a planet that is capable of supporting life, moreover we want a planet that could be Earth-like, this reason is for what we know now is that life can only develop on planets that are Earth-like. However for all we now their may be incredibly intelligent gaseous beings on a distant planet that has developed a highly technical civilization, we just do not know. However, we will denote this variable as E, for Earth-like planets. To put a number onto this I will just pluck a number completely out of the air and say only 10% of planets could be capable of sustaining life.


Just because the tools are there it does not mean that it will result in their being life. This variable is the fraction of Earth-like planets that do develop life, we will denote this L. However, I think a lot of the planets that are Earth-like will evolve life in some form, there is life at the very deepest depths of the ocean, there is life where a human would be completely obliterated within seconds. For this reason I think that if the planet has the means to sustain life, it often will, I estimate it will at least half of the time, so to be conservative I will put this variable at 0.5.


Again, just because there is life it doesn't mean that it will ever become 'intelligent' enough. Life may not have evolved as well on Earth had the dinosaurs not been wiped out, they may have never developed to an intelligent enough state to communicate using radio waves, they may have just stayed as a less intelligent being. This variable will then be the fraction of life that will develop into intelligent life, we will denote this as I. Now this will be far more rare than their just being life, and in fact there is not even a rough number we can apply to this, but just for the sakes of this let's say that 1% of life will at one stage become intelligent.


The next variable we need to consider is the fraction of these civilizations that communicate via a means that we will be able to detect, we will denote this variable as C. For example humans have been around and intelligent for around thousands of years, but only for the last 80 or so would we be able to be detected, this is because of the discovery of radio waves. So before that we were, as a civilization, undetectable. Also we may discover that in a few hundred years there are far more efficient and productive methods to communicate, other alien civilizations may already be using this. So let's say again, pulling numbers completely at random, that 10% of intelligent civilizations develop a means of communication that we can detect.


The last variable that we need to consider is the fraction the average time the civilization is able to communicate takes up of the average age of star system, we will call this T. How long a civilization is able to communicate is something that although we do not know (as we still exist, just!) we can estimate. We have only been able to communicate via radio waves for 80 years, and every single one of those has been riddled with war. However, I remain optimistic that we, and all intelligent life, should be able to last about 10,000 years in the state of communication. The average age of a start system is around 10 billion years. So the calculation to find T is 10,000/10,000,000,000, which as a decimal is 0.000001.


The equation that we now have, after considering all the things we need to look for is:
Number of Alien Civilizations = Number of Stars * Fraction of stars with Planets * Fraction of Earthlike Plants * * Fraction of Planets with Life * Fraction of Intelligent Planets * Ability to Communicate * (Lifetime of Planet)/(Lifetime of Star)


This is a lot of text for maths, so to put it algebraically:
N = S*P*E*L*I*C*T


Now if we input the estimates that I designated earlier we get:
N = 200,000,000,000 * 0.5 * 0.01 * 0.5 * 0.1 * 0.1 * 0.000001


Now if we do this calculation we get that in this case N = 5. So there should be about 5 alien civilizations that are detectable from my very estimated estimates.


But the point of this equation is not to come up with a concrete number of civilizations that we must be able to communicate with right now. But this equation gives us the types of data that we should be looking for if we want to know the potential amount of aliens in the galaxy. If we know what to be looking for to know how many potentially intelligent aliens could be in our galaxy we can hone our efforts in on what data we need to look for. Also, it is pretty cool to be able to estimate how many aliens are out there and able to be detected in our own galaxy, and what happens if we change certain variables, etc.


If you fancy estimating how many detectable lives our out there using the original Drake equation, try it out for yourself at WolframAlpha.

Maths and the Real World: Linear Programming

Linear Programming may be bread and butter to you or it may be an entirely new concept. But it is one of the most applicable pieces of maths that is used in every day life by business and companies alike, this of course is minimising costs and maximising profits.


I will propose a problem to you, you are a company that sells two types of fruit drinks that consists of fruit juice and sugar syrup. Juice A consists of 0.3 litres of fruit juice and 0.5 litres of syrup and Juice B consists of 0.6 litres of juice and 0.4 litres of syrup. You have 30,000 litres of juice and 40,000 litres of syrup already in your stock. The profit for Juice A is 20p and the profit for Juice B is 30p. Given this scenario, you wish to maximise your profit.


How would you go about doing this? Well let's begin by putting the information we have in a table and go from there.

	Fruit Juice (in litres)	Syrup (in litres)	Profit (in pence)
A	0.3	0.5	20
B	0.6	0.4	30
Total	20,000	30,000

Now, from this information we need to construct the constraints of the problem into mathematical terms. What inequality will represent the amount of fruit juice that is allowed to be used? Well it must be less than or equal to 30,000 that is clear, it also depends on how much of it is used by Juice A and Juice B, so if 0.3 of A is used each time Juice A is created, and 0.6 of B is used when Juice B is created. This then means that 0.3A+0.6B ≤ 30,000. Using the same rules we must concur that 0.5A+0.4B ≤ 40,000. Also we want to maximise the amount of profit that we make, this means that P = 20A+30B. But there are other less obvious constraints that we must consider. We can not use a negative amount of juice or syrup so A ≥ 0 and B ≥ 0.

To get an idea of what sort of values we can have we plot these inequalities onto a graph which will give us an idea of what values of A and B are actually possible to obtain.

The blue shaded region is the answers that are within
 the constraints of our inequalities. This is called the
region of feasibility.

So we have the region that the answers must be within, now we want to go about maximising the profit which has an equation of, P = 20A+30B. This will be the last point that the line P = 20A+30B touches on the region of feasibility, this means that what P actually equals is arbitrary as we only need to gradient of that line and it will then be moved until it touches the last point it possible can on the region of feasibility. So we will choose a number that is convenient to plot for us, I'll be using P = 600.

The line begins to gain opacity as it moves closer to the
further point on the region of feasibility. Point 'A' is the
 maximum point within the reason of feasibility, therefore
this is the maximum value.

We could try to read this point of the graph but it would far more accurate to solve this using where the point is met by the two equations and solve simultaneously. So we are solving the simultaneous equations of 0.3A+0.6B = 30,000 and 0.5A+0.4B = 40,000.

This then in the context means that to optimise the profit within our constraints we should make 200,000/3 litres of Juice A and 50,000/3 of Juice B. This then equates to about £6333, which is the maximum profit we can achieve from the circumstances we have been given.

This is just an example of how to use linear programming to optimise finances, but it is easily transferable to almost any situation. The only thing you may need to watch out for is if A and B are number of items that need to be sold, they must be whole numbers (obviously) so you may need to round and then check that this will still lie in the region of feasibility.

Again, I hope you find this interesting and in fact very applicable to real life. If you have any questions on anything I have done, how it works or even how I create my images, please comment and I will reply.

Limit of Sin(x)/x at x = 0

First, for those of you that do not know what a limit is, I will begin by defining it in more simple terms before getting into the more complex things. If a series is convergent that means it will tend to a limit. What is a limit? It is a value that a graph will get infinitely close to but will never quite reach. For example the limit as x approaches infinity of 1/x is 0. This can be more concisely denoted as:

Which means that a broad way to right the limit of anything is:

This is where c is a real number, f(x)  a function and L is the limit of that function.


But as my last example shows, it is not just series that can tend to a limit, functions can also have a limit when the function is undefined at a point. In fact limits are vital to such a massive part of mathematics, you will not be able to go into a career or a path within maths without encountering limits. It is so important to calculus that it is required in the proof that an indefinite integral can be reversed by differentiation. If you're interested in that you can read it here.


Now that we have our definition we can begin an explanation of the limit of Sin(x)/x as x approaches 0. The proof is a visual one, so there will be a lot of images to emphasise my explanations.


We will begin by taking the unit circle, a circle with a radius 1 and a centre (0,0), (an equation of x²+y²=1). And begin constructing a variety of triangles, it is much easier to show this as an image. The one thing I must point out is that x in an angle in radians.

Next we will begin to label the lengths of every side that we possibly can. Anything that is a radius will be 1 (the radius of a unit circle is 1). Once we have that we can begin to use trigonometry to find the values of the other sides.

The height of the triangle opposite angle using the well known SOHCAHTOA rule can be found to be: Sin(x)/1, which is equivalent to Sin(x). This then means the area of the triangle with base 1 will be; 0.5*1*Sin(x), or Sin(x)/2.


To find the area of the segment of the triangle we will use the formula to find the area of a segment, 0.5*r²*x; r = 1 so we can find the area of the segment to be x/2.


There is one final side we will want to find to find the area of. The height of the largest vertical line. Again using SOHCAHTOA we can find this side to be Tan(x). This then means that the area of this triangle is 0.5*1*Tan(x), or Tan(x)/2.

What I have just described is represented
 visually here with the equations of the shaded
 shapes listed.

This then means (as we can see visually) that the green area is less than the red and green area which is less than the blue, red and green area. This then means that: Sin(x)/2 < x/2 < Tan(x)/2. If we times through by 2 this means that, Sin(x) < x < Tan(x). Now if we divide the whole expression by Sin(x) we get Sin(x)/Sin(x) < x/Sin(x) < Tan(x)/Sin(x). Sin(x)/Sin(x) = 1, x/Sin(x) can not be simplified but Tan(x)/Sin(x) can be.


Tan(x) can be represented as Sin(x)/Cos(x), inputting this back into the equation gives us: Sin(x)/Cos(x)/Sin(x) which equals 1/Cos(x). So we now have 1 < x/Sin(x) < 1/Cos(x). You can see we are getting near to Sin(x)/x now, all we need to do is invert the whole expression, this will flip the inequality signs to compensate.


So 1 > Sin(x)/x > Cos(x). Now we will use something called the squeeze theorem to find Sin(x)/x. If we have an inequality a < b < c and a = c, then b must then be equal to both a and c. So we need to find the limit of 1 and Cos(x) as x approaches 0. No matter what x approaches for 1 it will never change from 1, and as x approaches 0 of Cos(x) we get Cos(0) which also equals 0.


This then means that 1 < Sin(x) < 1, so Sin(x) must also equal 1. Our proof is now complete, this therefore means that as x approaches 0 of Sin(x)/x is 1.

If you found my calculations hard to follow in the form of text, look other them below (comments on what is happening are boxed):

I hope you managed to follow all of that, but if you didn't or you need any further explanation on any part of this please, please comment and I will get back to you.

Sequences and Series

In maths a sequence is an ordered list of numbers called objects, a sequence can be finite, infinite or bi-infinite. A finite sequence is easy to define it is simply a set of finite numbers (for example 1, 3, 5, 7 is a finite sequence); an infinite sequence is slightly harder to picture but it also makes sense, it is simply a sequence that does not terminate at any point (for example the natural numbers start are 1, 2, 3... and will never cease) and a bi-infinite sequence may be a slightly newer concept to try and grasp but it is equally easy to understand, it stretches infinitely in both directions (for example the integers are a bi-infinite sequence ...-2, -1, 0, 1, 2... as it will never cease in either direction).

The sum of a sequence is a series, and this is where the real fun of it all begins to come through with sequences. Often we look to see whether a series is divergent, convergent or oscillating, what this means is whether the series will converge to a limit, if it is divergent it will just get larger and larger in either the positive or negative direction and if a series is oscillating it neither converges to a limit nor diverges to infinity (for example: 1, -1, 1, -1, ... will not converge or diverge, thus it is oscillating).



It is also possible to find the sum of an arithmetic and geometric series (these will be defined later), but first I'll have to introduce some concepts of the symbols used when talking of the sums of numbers. If we have a function, f(x), our first term is, r, and we want to go up to term, n. The way you would usually do this long hand and have to do f(r)+f(r+1)+...+f(n-1)+f(n), but this can be more concisely wrote as:

As you can see this is far easier to write and is just as easy to interpret. But how actually do you find the sum of a series?


For example if we wanted to find the sum to the first 10 natural numbers, 1+2+3+4+5+6+7+8+9+10, what way could we find the answer relatively quickly? Pairing the numbers up first and last, second and second last, etc. will mean each number will be the same so makes an easier calculation. If we do that we get (1+10)+(2+9)+(3+8)+(4+7)+(5+6), which is 11+11+11+11+11 (or better represented as 11*5). So the sum of the first 10 natural numbers is 55.


We can write this short hand by finding out how many pairs their will be and what each one will equal, or S = 0.5n(a+l), where n is the number of terms, a is the first term and l is the last term. Another way of writing this (when we do not know the last term) is that l = a+(n-1)d, if you want an explanation on this please comment. This then means that the sum of an arithmetic series is, S = 0.5n(2a+(n-1)d). **Note that these last two paragraphs only apply to arithmetic series**


We can also find the sum of a geometric sequence (a term starts with 'a' and is the increased by 'r', so the next will be 'ar' and the third will be 'ar²' etc.). This means that the nth term of the sequence will be, ar^n-1. So to find the sum of a geometric progression, let us consider that S_n = a+ar+ar²+...+ar^n-1, if we multiply through by r we get rS_n = ar+ar²+...+arⁿ, if we take the first from the second we get: S_n-rS_n = a-arⁿ, which can be represented as S_n(1-r) = a-arⁿ, dividing through by (1-r) we get the formula for the sum of a geometric progression:

Now we can use this to find the sum to infinity of geometric progression (provided that -1<r<1), it will mean that will arⁿ approach 0 as n approaches infinity, when we have that it becomes easy to find the new equation:

There are also other elements to this general topic, but I think they warrant a topic in their own right. I briefly cover the definition of what a limit is here.

AS and GCSE Maths Free Tuition

I am offering free help to anyone who needs it on any GCSE or AS Maths (I am best at C1, C2 and FP1; but can help at any). If you need any help on any of these, or just a general mathematical query, just leave a comment here and I will try to explain here and if you need long term support I will provide you with my email address and we can talk more regularly there. So what are you waiting for? Post your questions now!