AS Maths Core 1: Polynomials

Poly, as you may or may not know, means many, and nomial as you likely will not know means terms. Put this together and we get many terms, and that really is the definition of a polynomial. This topic is reasonably large, but none of it is too difficult and it is easy marks to gain in the exam as long as you are careful and know your stuff!

Quadratic Equations

Discriminant
The discriminant of a quadratic equation is something that can tell you how many real roots a quadratic equation will have. If we look at the quadratic equation we know that that you can only find the square root of a positive integer (and zero). The discriminant is what is being square rooted in the quadratic equation (b²-4ac).

If the discriminant is greater than 0 then the quadratic would have two distinct real roots (it crosses the x-axis twice), if the discriminant is equal to 0 then there is one repeated real root (it just touches the x-axis once, at its vertex) and if the discriminant is less than 0 then there are no real roots (it will not touch the x-axis).


If b²-4ac > 0 then the quadratic has two distinct real roots.

If b²-4ac = 0 then the quadratic has one repeated real root.

If b²-4ac < 0 then the quadratic has no real roots.

Quadratic Inequalities
Now, quadratic inequalities can be pretty tricky if you never spent enough time learning them, but if you do spend enough time doing you will be able to get full marks on them every time. First of all the general form of a quadratic inequality is: ax²+bx+c > 0 or ax²+bx+c < 0, note that the signs could also be ≥ or ≤, but this makes no difference in the method but you just need to ensure you use the correct sign in your final answer.

The first thing you need to do is solve the equation equal to zero to get the points that the quadratic crosses the x-axis. Once you have this you need to sketch the quadratic and the shade the side of the quadratic where it is either <0 or 0<. If the quadratic has the sign like this:  ax²+bx+c > 0, you will need to shade only about the x-axis (as that is where y>0), if the inequality is the other way,  ax²+bx+c < 0, then you need to shade below the x-axis (as that is where y<0). It is then easy to see what values the inequality will satisfy.

Example:
Find the range of values that satisfy the inequality,  x²+6x+8 < 0
We’ll begin by solving the equation equal to 0.x²+6x+8, this is then factorised to (x+2)(x+4) = 0, so the quadratic crosses the x-axis at (-2,0) and (-4,0).
Plotting this graph and then shading where the graph is less than 0.

This then means that the inequalities range of results is when x>-4 and x<-2, this can be wrote as a continuous set of values, -4<x<-2.

Note that if the inequality is of the form ax²+bx+c < 0, it will always be a continuous set of values. If it is of the form ax²+bx+c > 0, it will not be a continuous set of values, ever.


Complete the Square
This method of solving quadratics is itself not exactly too efficient and if the quadratic is an awkward one it is often much simpler to use the quadratic formula (which was derived from completing the square) to solve it. But it does have other very useful properties, most of which you will be required to learn.

I will begin by talking you through the steps of how you complete the square of anything.
ax²+bx+c = 0
If we divide the expression through by ‘a’ we get:
x²+(b/a)x+(c/a) = 0
Now if we want to get a perfect square (hence complete the square) we must half the second term, square it, add it on and take it away:
x²+(b/a)x+(b/2a)²-(b/2a)²+(c/a) = 0
Which we can then simplify into the following form:
(x+(b/2a))²-(b/2a)²+(c/a) = 0

Now if you are observant you will see that what is in the bracket with the x is the original number we halved. This will always be the case. Also you should note that -(b/2a)²+(c/a) will be combined as they will both be real numbers.

Now we have our general form of a quadratic in a completed square form, (x+(b/2a))²-(b/2a)²+(c/a) = 0, what can we actually do with it? We can use it to find the vertex of a quadratic equation, going from our example the vertex would be (-(b/2a), -(b/2a)²+(c/a)) . Now this looks pretty confusing but when you apply it to an actual equation it is incredibly easy.

Example:
Find the vertex of 2x²+8x+4=0.
We begin by dividing through by 2 to get, x²+4x+2=0
Halving 4 gives us 2, so our new equation must be:
(x+2)² - 2² + 2 = 0
And on simplifying we get: (x+2)² - 2 = 0
So the vertex must be at (-2, -2)

And it is as easy as that! The only other thing you must know for completing the square is how you change x² into x²+bx+c, and this really is just an extension of completing the square. The vertex of x² is (0,0), so if the vertex of a quadratic is say, (a, b) then the graph of x² is TRANSLATED by 


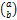
Using our worked example again:
Find the transformation that maps 2x² onto 2x²+8x+4=0

Using our vertex from the previous example, (-2,-2)
This means that x² is translated by 

Remainder Theorem
This again, is very, very easy to do. You just have to watch out for very small errors when doing your calculations and that you do not make an error straight away. To check the remainder when f(x) is divided by (x+a) we get the notation of f(-a), so wherever there is an x in the expression we put a ‘-a’. Whatever this then equals to is the remainder when f(x) is divided by (x+a). This really is all there is to it.

Example:
Find the remainder when f(x) = x³+3x²-6x+4 is divided by (x+2).
f(-2) = (-2)³+3(-2)²-6(-2)+4
f(-2) = -8+12+12+4
f(-2) = 20
Therefore when x³+3x²-6x+4 is divided by (x+2) the remainder is 20.

Factor Theorem
The Factor Theorem is just a special case of the remainder theorem; this is when the remainder of that is equal to 0. For example 6/2 has a remainder of 0 therefore 2 is a factor of 6 (obviously). So (x+a) is a factor of f(x) when f(-a) = 0.

Example:

Verify that (x+2) is a factor of f(x) = x³+4x²+x-6.
f(-2) = (-2)³+4(-2)²+(-2)-6
f(-2) = -8+16-2-6 = 0
f(-2) = 0, therefore (x+2) is a factor of f(x)

Algebraic Long Division
Often you will have one factor of a cubic equation and need to find the other factors. Now there are other ways to do this (factor theorem, solving by inspection, etc.) but personally I find that algebraic long division is the most efficient and accurate way of finding the other factors.

You will only be dealing with factors of the form (x+a), it will never be (2x+a), etc. So it never gets too complicated. I will explain what you need to do with an example.

Now, this is something that might be quite hard to get your head around at first, and you really need to just practice as much as you can. You also need to know that often the quadratic formed can be further factorised. This is true in our example, so representing x³-2x²-5x+6 as a product of three linear factors is: (x+2)(x-1)(x-3). If you have an equation where there is no say 'x' term or 'x²' term you must when dividing it make it 0x² or 0x.

Sketching Graphs

Often you will be required to sketch the graph of a quadratic or a cubic once you have found the roots of the polynomial. There are a few things you have to make sure you do, if you do them you will always get the marks for the quadratic.

• Always mark the points where the polynomial crosses the x-axis and the y-axis.
•  Draw the axes with a ruler.
• Draw the polynomial smoothly; do not draw it bit by bit.
• If you need to draw a line on the graph as well, mark all points of intersection (with graph and axes).
• Make sure you use a pencil in case of mistakes.
• Draw the graph a reasonable size, (I’d go for at least a third of a page if not more).
• Make sure that the shape is roughly correct and resembles the correct polynomial.
• Get the minimum point in roughly the right area.

My advice would be roughly work out where each point is going to be, draw it with a fluid action and then mark the points of intersection on.

And that is it for my guide on polynomials in Core 1, I have taken this from my upcoming eBook revision guide for Core 1, the eBook will also include questions, answers and far more detail. Keep checking back for more.