Limit of Sin(x)/x at x = 0

First, for those of you that do not know what a limit is, I will begin by defining it in more simple terms before getting into the more complex things. If a series is convergent that means it will tend to a limit. What is a limit? It is a value that a graph will get infinitely close to but will never quite reach. For example the limit as x approaches infinity of 1/x is 0. This can be more concisely denoted as:

Which means that a broad way to right the limit of anything is:

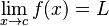
This is where c is a real number, f(x)  a function and L is the limit of that function.


But as my last example shows, it is not just series that can tend to a limit, functions can also have a limit when the function is undefined at a point. In fact limits are vital to such a massive part of mathematics, you will not be able to go into a career or a path within maths without encountering limits. It is so important to calculus that it is required in the proof that an indefinite integral can be reversed by differentiation. If you're interested in that you can read it here.


Now that we have our definition we can begin an explanation of the limit of Sin(x)/x as x approaches 0. The proof is a visual one, so there will be a lot of images to emphasise my explanations.


We will begin by taking the unit circle, a circle with a radius 1 and a centre (0,0), (an equation of x²+y²=1). And begin constructing a variety of triangles, it is much easier to show this as an image. The one thing I must point out is that x in an angle in radians.

Next we will begin to label the lengths of every side that we possibly can. Anything that is a radius will be 1 (the radius of a unit circle is 1). Once we have that we can begin to use trigonometry to find the values of the other sides.

The height of the triangle opposite angle using the well known SOHCAHTOA rule can be found to be: Sin(x)/1, which is equivalent to Sin(x). This then means the area of the triangle with base 1 will be; 0.5*1*Sin(x), or Sin(x)/2.


To find the area of the segment of the triangle we will use the formula to find the area of a segment, 0.5*r²*x; r = 1 so we can find the area of the segment to be x/2.


There is one final side we will want to find to find the area of. The height of the largest vertical line. Again using SOHCAHTOA we can find this side to be Tan(x). This then means that the area of this triangle is 0.5*1*Tan(x), or Tan(x)/2.

What I have just described is represented
 visually here with the equations of the shaded
 shapes listed.

This then means (as we can see visually) that the green area is less than the red and green area which is less than the blue, red and green area. This then means that: Sin(x)/2 < x/2 < Tan(x)/2. If we times through by 2 this means that, Sin(x) < x < Tan(x). Now if we divide the whole expression by Sin(x) we get Sin(x)/Sin(x) < x/Sin(x) < Tan(x)/Sin(x). Sin(x)/Sin(x) = 1, x/Sin(x) can not be simplified but Tan(x)/Sin(x) can be.


Tan(x) can be represented as Sin(x)/Cos(x), inputting this back into the equation gives us: Sin(x)/Cos(x)/Sin(x) which equals 1/Cos(x). So we now have 1 < x/Sin(x) < 1/Cos(x). You can see we are getting near to Sin(x)/x now, all we need to do is invert the whole expression, this will flip the inequality signs to compensate.


So 1 > Sin(x)/x > Cos(x). Now we will use something called the squeeze theorem to find Sin(x)/x. If we have an inequality a < b < c and a = c, then b must then be equal to both a and c. So we need to find the limit of 1 and Cos(x) as x approaches 0. No matter what x approaches for 1 it will never change from 1, and as x approaches 0 of Cos(x) we get Cos(0) which also equals 0.


This then means that 1 < Sin(x) < 1, so Sin(x) must also equal 1. Our proof is now complete, this therefore means that as x approaches 0 of Sin(x)/x is 1.

If you found my calculations hard to follow in the form of text, look other them below (comments on what is happening are boxed):

I hope you managed to follow all of that, but if you didn't or you need any further explanation on any part of this please, please comment and I will get back to you.