Algorithm to find the mth root of a number

I did in fact work this algorithm for myself and was reasonably proud at discovering this, only on a later Google search did I realise that the Babylonians discovered the exact same method almost 3000 years ago, my joy was obviously cut short but it is still a pretty cool algorithm nonetheless.

To start with I began thinking what needed to be done to calculate the mth root, I knew it had to be a method that did not involve having to find the root of anything, which means I needed to rewrite the question in a form that can be solved.

But as you may realise, this is no use as it is solely in terms of L. If you have done anything on recurrence relations and sequences and series you will see that L is merely the limit of the series, this limit will be mth root of x.

And that really is it, this gives an equation to find the mth root of any given number, x.

You can try it out for yourself and see how accurate it is, and for square roots (and even cube roots) it converges pretty quickly but as m increases the series converges much slower and is then not very appropriate to use. Also U₀ can be anything, the closer to the correct answer the better as it speeds the overall process up.

Infinite Circles Problem

I recently encountered a mathematical problem from NRich Maths about inscribed circles in an equilateral triangle and it really intrigued and after a little bit of intense thought I managed to figure it out.


For those of who wish to know what the problem is without clicking the link:

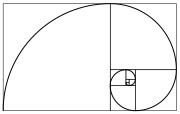
A circle of radius 1 cm is inscribed in an equilateral triangle. A smaller circle is inscribed at each vertex touching the first circle and tangent to the two 'containing' sides of the triangle. This process is continued ad infinitum...
 

What is the sum of the circumferences of all the circles?

What is the sum of their areas?

Adding all the circumferences or adding all the areas, which sum grows faster?

Now this might not be immediately obvious as the best way to approach this problem, so we need to think about what we know, what we need to know and the best way to approach this.


What We Know:

1. The radius of the largest circle is 1cm.
2. All of the triangles angles are 60° as the triangle is an equilateral.
3. The area of the first circle is π, the circumference is 2π.

What We Need To Know:

1. The ratio of the radii from each circle to the next.
2. The height of the triangle.
3. The area of all the circles.
4. The circumference of all the circles.

The height of the triangle may seem like a bit of a strange necessity, but if you know the diameter of the main circle (2cm) then it helps to know what the sum of the diameters of all of the circles will be (height-2).

Now if the the radius were arranged so it was at a right angle to the triangle and a line was drawn from the centre of the largest circle the corner of the side the radius touches the angle would be half of the original angle which is 60° so the new angle is 30°. This is hard to picture but an angle will help that.

Now we have two angles and one side, so we can use the Sin rule to find the size of the line from the centre of the circle to the corner of the triangle.

This means that the radius of the largest circle plus the diameters of all of the other circles is 2. So the height of the triangle 2 plus the radius of the larger circle, which equals 3. It also means that the sum of the diameters of all of the other circles equals 1 too.

Now we can begin to actually tackle the problem of the sum of the circumferences of all the circles. We already know that the circumference of the first circle is 2π, if the sum of all the diameters of the other circles in one line is 1 we can see that the area is then π, but we still have two other sets of circles. So we have the total circumference of 2π+π+π+π which means the total circumference is 5π. Problem one solved.

The second problem is slightly more awkward as the radius is not as easy to find and although the way I am about to explain does work in may not be the most efficient, but it does work and it utilises some very nice Core 2 techniques.

As you may have noticed, there will be an infinite number of circles going into any of the corners (this is caused by the curved shape of a circle against the straight side of the triangle). If we exclude the large circle then the sum of the diameters of into one corner is 1.

The fact that the triangles always get smaller, means that the rate at which they 'increase' is less than 1, we will call this ratio 1/n, the radius of the second triangle will also be 1/n because of the fact that the first radius is 1.

We know that the sum of the diameters equals 1, which means that the sum of 2*radius is also equal to 1. We also know the first term of this series (1/n), the ratio of the series (1/n) and the sum of the series (1). As our ratio is less than 0 we can use the formula covered in C2 for that:

Using that we can rearrange to find what n equals and thus find the ratio. I have included the original equilateral triangle image along with some labelling to help to explain my notation.

So we have that the ratio from radius to radius is 1/3, so to find the sum of the area of all the triangles we must use the sum of an infinite series again. Given that the first term is π (from πr^2 and r = 1), the ratio is r^2, which gives 1/9. We have three of the series so we will times the sum of these by 3, but then we have included the largest triangle three times, so we must subtract this two times (-2π).

This means that the area of all the circles is 11π/8, problem two solved.

The last problem is considerably easy to handle, it simply asks which sum grows faster, this is the one that has a larger ratio. Well the ratio of the area is 1/9, whereas the circumference is 2/3 (r is 1/3, but we want twice this). So this means the circumference increases faster.

This problem really is a lovely one, it combines some relatively simple maths in an advanced form, pieces them all together and leaves you to solve the puzzle. Maths is fun. Maths is really, really fun!

I realise I may have explained fair chunks of this poorly, it is very difficult to convey what is happening and without being in front of you. So if you are left with any questions as to what I have done, or why, simply leave a comment and I will explain or email me at lewis.mead@eloquentmath.com for more information.

Also to let you know, I will be completing a Core 2 revision guide pretty soon (give me a week or so), so keep checking back here for updates on that.

Sequences and Series

In maths a sequence is an ordered list of numbers called objects, a sequence can be finite, infinite or bi-infinite. A finite sequence is easy to define it is simply a set of finite numbers (for example 1, 3, 5, 7 is a finite sequence); an infinite sequence is slightly harder to picture but it also makes sense, it is simply a sequence that does not terminate at any point (for example the natural numbers start are 1, 2, 3... and will never cease) and a bi-infinite sequence may be a slightly newer concept to try and grasp but it is equally easy to understand, it stretches infinitely in both directions (for example the integers are a bi-infinite sequence ...-2, -1, 0, 1, 2... as it will never cease in either direction).

The sum of a sequence is a series, and this is where the real fun of it all begins to come through with sequences. Often we look to see whether a series is divergent, convergent or oscillating, what this means is whether the series will converge to a limit, if it is divergent it will just get larger and larger in either the positive or negative direction and if a series is oscillating it neither converges to a limit nor diverges to infinity (for example: 1, -1, 1, -1, ... will not converge or diverge, thus it is oscillating).



It is also possible to find the sum of an arithmetic and geometric series (these will be defined later), but first I'll have to introduce some concepts of the symbols used when talking of the sums of numbers. If we have a function, f(x), our first term is, r, and we want to go up to term, n. The way you would usually do this long hand and have to do f(r)+f(r+1)+...+f(n-1)+f(n), but this can be more concisely wrote as:

As you can see this is far easier to write and is just as easy to interpret. But how actually do you find the sum of a series?


For example if we wanted to find the sum to the first 10 natural numbers, 1+2+3+4+5+6+7+8+9+10, what way could we find the answer relatively quickly? Pairing the numbers up first and last, second and second last, etc. will mean each number will be the same so makes an easier calculation. If we do that we get (1+10)+(2+9)+(3+8)+(4+7)+(5+6), which is 11+11+11+11+11 (or better represented as 11*5). So the sum of the first 10 natural numbers is 55.


We can write this short hand by finding out how many pairs their will be and what each one will equal, or S = 0.5n(a+l), where n is the number of terms, a is the first term and l is the last term. Another way of writing this (when we do not know the last term) is that l = a+(n-1)d, if you want an explanation on this please comment. This then means that the sum of an arithmetic series is, S = 0.5n(2a+(n-1)d). **Note that these last two paragraphs only apply to arithmetic series**


We can also find the sum of a geometric sequence (a term starts with 'a' and is the increased by 'r', so the next will be 'ar' and the third will be 'ar²' etc.). This means that the nth term of the sequence will be, ar^n-1. So to find the sum of a geometric progression, let us consider that S_n = a+ar+ar²+...+ar^n-1, if we multiply through by r we get rS_n = ar+ar²+...+arⁿ, if we take the first from the second we get: S_n-rS_n = a-arⁿ, which can be represented as S_n(1-r) = a-arⁿ, dividing through by (1-r) we get the formula for the sum of a geometric progression:

Now we can use this to find the sum to infinity of geometric progression (provided that -1<r<1), it will mean that will arⁿ approach 0 as n approaches infinity, when we have that it becomes easy to find the new equation:

There are also other elements to this general topic, but I think they warrant a topic in their own right. I briefly cover the definition of what a limit is here.

Fibonacci Sequence

A sequence of integer numbers that after its first two numbers each subsequent term is the sum of the previous two terms: F_n=F_n-1+F_n-2

. The sequence is then of course infinite. The first 10 terms of the sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34

Now this in itself is not a very difficult or overly interesting/complex sequence. But the huge array of implications it has on the "real world" are incredibly interesting and in fact fascinating, if you're a nerd that is.

 

This is the Fibonacci tile, each square has the side length of what's in the middle of the square. Pretty but so what? Well, as all Mathematicians are, they weren't content with just turning a sequence into an array of squares and they looked deeper, don't they always? If you make a quarter circle from the tangents of each square and continue this way going through each square you end up with a spiral, obviously.

Oooh pretty, but big woop? Well yes, actually quite a massive big woop in fact. It is staggering how often either the Fibonacci spiral or sequence appears in nature. The branches of trees, arrangement of leaves, the flowering arrangements of certain flowers, the arrangement of a pine cone, the spiral of shells, the curvature of waves and even in family tree of bees, seriously. If you want to read about how the hell they're related please go here: http://en.wikipedia.org/wiki/Fibonacci_spiral#In_nature

Bees and the Fibonacci sequence, a match made in heaven. I'm waiting for my image to hit the papers, I'm pretty certain it will be voted the Scientific Breakthrough of the Year.

Other Random Facts:

Every positive integer can be wrote in a unique way as the of one or more Fibonacci terms and it will not include any two consecutive Fibonacci terms.

The Fibonacci Sequence can be used to determine tunings in music.

The Golden Ratio and Fibonacci Sequence are very, very closely related.