Modular arithmetic is an arithmetic system for the integers where the numbers wrap around, like on a clock for example. The numbers start at one, they go round to twelve and then start again at one, this would be an example of modulo 12. However generally in modular arithmetic we start at 0 and go to 11, before starting at 0 again. This means that 7 o'clock would be 6 mod 12 (mod is often used to shorten modulo). In fact because the number line "wraps around" it means that 19 o'clock = 7 o'clock (as you will know if you have used a 24 hour clock), this means that 18 mod 12 = 6 mod 12; because of this a mod m is wrote where a < m.
However it does not have to be just modulo 12, it can be modulo anything (as long at is a positive integer), so let us jump straight into the definition. So that you are aware of the notation I will use a|b means b divides a (this means that b/a is an integer). Let m be a positive integer and let a, b both be integers if m|a-b then a is congruent to b modulo m, wrote mathematically this is: a ≡ b mod m. Make sure you do not think "≡" means equivalent in this case, because it does not!
You can add in modular arithmetic (provided they have the same modulo). Let m be a positive integer and let a, b,c and d be integers if a ≡ b mod m and c ≡ d mod m then a + c ≡ (b+d) mod m. So basically you add the parts preceding the modulo together and then find modulo m of that.
You may also notice that a/m has a remainder of b, this is how we can quickly work out that 19 o'clock is the same as 7 o'clock, or the same as 103 o'clock. You simple divide the number by the modulo and work out the remainder.
An example of why we would use this using our clock as an example is if it is 4 o'clock now, what will the time be in 157 hours? So what we have is 3 mod 12 and 157 mod 12, adding these together we get 160 mod 12, 160/12 = 13 remainder 4. This means that 160 mod 12 = 4 mod 12, so it will be 5 o'clock 157 hours from 4 o'clock.
This should give you an idea of how to do basic addition with congruences, if you do not understand fully read what I have wrote again and then if you still do not understand, post a comment. Now we have the basic principles in place we can begin to go further. Now we will prove that a mod m + b mod m = (a+b) mod m and also how multiplication works in modular arithmetic.
Multiplication between two congruences is just as easy as addition with congruences, I will first provide a definition to you, before proving it. Let m be a positive integer and let a, b,c and d be integers if a ≡ b mod m and c ≡ d mod m then ac ≡ (bd) mod m; this is the same sort of principle as addition. Now to prove them.
First to prove addition:
Now to prove multiplication:
These are the very basics of congruences, but the are integral to modular arithmetic (I mean, think how important addition and multiplication is normally), they are very, very powerful and I will begin to explore them more and more in my upcoming posts. I will prove just one more result as it is pretty easy and uses multiplication.
The proposition is that an ≡ bn mod m is also true provided a ≡ b mod m and n is a positive integer. We will prove this by induction. Let P(n) be be the statement of the proposition, then P(1) is obviously true as we already know that a ≡ b mod m. So let us assume that P(n) is true, then we have that an ≡ bn mod m and that a ≡ b mod m, multiplying the two of them together (using our proved method) we get a × an ≡ b
× bn mod m, this then simplifies to: an+1 ≡ bn+1 mod m, which is P(n+1). Hence P(n) is true for all values of n!
I hope that you like this post and that is helps you. If you did like it then please also like us on Facebook.
Showing posts with label amazing. Show all posts
Showing posts with label amazing. Show all posts
Sunday, 26 February 2012
Monday, 13 February 2012
Proof by Contradiction: Infinite Prime Numbers
There are many complex and obscure methods of proving that there are infinite prime numbers, but this one is certainly the easiest and it is a demonstration of how unpredictable numbers can be dealt with in an efficient manner, it is also an easy introduction to proofs by contradiction.
First, just to clarify what proof by contradiction actually means:
1.) We assume that what we are trying to prove to be false is in fact true.
2.) If we find a contradiction in our assumed hypothesis that we have assumed then it can not be true. And that means that our assumed hypothesis is false, proving what we originally wanted.
So using this as our basis we are going to assume that there is in actual fact a finite amount of prime numbers, how many there is does not matter just that at some point there are no more prime numbers. If we multiply all of these prime numbers together we will get:
2 × 3 × ... × pn-1 × pn
Where pn is the last prime number and this number is clearly not prime as is has every single prime number as a factor. However if we add 1 to this number then any of the prime numbers that we try to divide it by will give a remainder of 1, this means that it too is prime!
p = 2 × 3 × ... × pn-1 × pn + 1
If this number is also prime it means that our original statement about there being finite prime numbers is incorrect, therefore there are an infinite number of prime numbers!
This took literally two lines of working to prove that there are an infinite number of prime numbers, this massive, beautiful and unfathomable concept was proved so efficiently and beautifully. This is what Maths is about, how concisely you can express complicated statements. Maths is solely about explaining the world around us and where this leads us is some amazing, incomprehensible places.
First, just to clarify what proof by contradiction actually means:
1.) We assume that what we are trying to prove to be false is in fact true.
2.) If we find a contradiction in our assumed hypothesis that we have assumed then it can not be true. And that means that our assumed hypothesis is false, proving what we originally wanted.
So using this as our basis we are going to assume that there is in actual fact a finite amount of prime numbers, how many there is does not matter just that at some point there are no more prime numbers. If we multiply all of these prime numbers together we will get:
2 × 3 × ... × pn-1 × pn
Where pn is the last prime number and this number is clearly not prime as is has every single prime number as a factor. However if we add 1 to this number then any of the prime numbers that we try to divide it by will give a remainder of 1, this means that it too is prime!
p = 2 × 3 × ... × pn-1 × pn + 1
If this number is also prime it means that our original statement about there being finite prime numbers is incorrect, therefore there are an infinite number of prime numbers!
This took literally two lines of working to prove that there are an infinite number of prime numbers, this massive, beautiful and unfathomable concept was proved so efficiently and beautifully. This is what Maths is about, how concisely you can express complicated statements. Maths is solely about explaining the world around us and where this leads us is some amazing, incomprehensible places.
Thursday, 15 December 2011
Infinite Circles Problem
I recently encountered a mathematical problem from NRich Maths about inscribed circles in an equilateral triangle and it really intrigued and after a little bit of intense thought I managed to figure it out.
For those of who wish to know what the problem is without clicking the link:
What We Know:
For those of who wish to know what the problem is without clicking the link:
A circle of radius 1 cm is inscribed in an equilateral triangle. A smaller circle is inscribed at each vertex touching the first circle and tangent to the two 'containing' sides of the triangle. This process is continued ad infinitum...Now this might not be immediately obvious as the best way to approach this problem, so we need to think about what we know, what we need to know and the best way to approach this.

What is the sum of the circumferences of all the circles?What is the sum of their areas?Adding all the circumferences or adding all the areas, which sum grows faster?
What We Know:
- The radius of the largest circle is 1cm.
- All of the triangles angles are 60° as the triangle is an equilateral.
- The area of the first circle is π, the circumference is 2π.
What We Need To Know:
- The ratio of the radii from each circle to the next.
- The height of the triangle.
- The area of all the circles.
- The circumference of all the circles.
The height of the triangle may seem like a bit of a strange necessity, but if you know the diameter of the main circle (2cm) then it helps to know what the sum of the diameters of all of the circles will be (height-2).
Now if the the radius were arranged so it was at a right angle to the triangle and a line was drawn from the centre of the largest circle the corner of the side the radius touches the angle would be half of the original angle which is 60° so the new angle is 30°. This is hard to picture but an angle will help that.
Now we have two angles and one side, so we can use the Sin rule to find the size of the line from the centre of the circle to the corner of the triangle.
This means that the radius of the largest circle plus the diameters of all of the other circles is 2. So the height of the triangle 2 plus the radius of the larger circle, which equals 3. It also means that the sum of the diameters of all of the other circles equals 1 too.
Now we can begin to actually tackle the problem of the sum of the circumferences of all the circles. We already know that the circumference of the first circle is 2π, if the sum of all the diameters of the other circles in one line is 1 we can see that the area is then π, but we still have two other sets of circles. So we have the total circumference of 2π+π+π+π which means the total circumference is 5π. Problem one solved.
The second problem is slightly more awkward as the radius is not as easy to find and although the way I am about to explain does work in may not be the most efficient, but it does work and it utilises some very nice Core 2 techniques.
As you may have noticed, there will be an infinite number of circles going into any of the corners (this is caused by the curved shape of a circle against the straight side of the triangle). If we exclude the large circle then the sum of the diameters of into one corner is 1.
The fact that the triangles always get smaller, means that the rate at which they 'increase' is less than 1, we will call this ratio 1/n, the radius of the second triangle will also be 1/n because of the fact that the first radius is 1.
We know that the sum of the diameters equals 1, which means that the sum of 2*radius is also equal to 1. We also know the first term of this series (1/n), the ratio of the series (1/n) and the sum of the series (1). As our ratio is less than 0 we can use the formula covered in C2 for that:
Using that we can rearrange to find what n equals and thus find the ratio. I have included the original equilateral triangle image along with some labelling to help to explain my notation.
So we have that the ratio from radius to radius is 1/3, so to find the sum of the area of all the triangles we must use the sum of an infinite series again. Given that the first term is π (from πr^2 and r = 1), the ratio is r^2, which gives 1/9. We have three of the series so we will times the sum of these by 3, but then we have included the largest triangle three times, so we must subtract this two times (-2π).
This means that the area of all the circles is 11π/8, problem two solved.
The last problem is considerably easy to handle, it simply asks which sum grows faster, this is the one that has a larger ratio. Well the ratio of the area is 1/9, whereas the circumference is 2/3 (r is 1/3, but we want twice this). So this means the circumference increases faster.
This problem really is a lovely one, it combines some relatively simple maths in an advanced form, pieces them all together and leaves you to solve the puzzle. Maths is fun. Maths is really, really fun!
I realise I may have explained fair chunks of this poorly, it is very difficult to convey what is happening and without being in front of you. So if you are left with any questions as to what I have done, or why, simply leave a comment and I will explain or email me at lewis.mead@eloquentmath.com for more information.
Also to let you know, I will be completing a Core 2 revision guide pretty soon (give me a week or so), so keep checking back here for updates on that.
Wednesday, 7 December 2011
Riemann Hypothesis
Now I am definitely not an expert in this field, and in fact even the experts aren't really experts in the conventional sense. No one is an expert on it in the conventional sense, it is still unsolved. Over 150 years old and it still remains unsolved not for the lack of trying! In fact it is so important to mathematicians that the Clay Mathematics Institute has put a $1,000,000 bounty on its head (that is, you get $1,000,000 if you manage to solve it).
But what actually is the Riemann Hypothesis? It is a conjecture about the location of the non-trivial zeros of the Riemann Zeta function, it states that all the zeros should lie on the critical strip 0.5+it. "Oh yeah!", I hear you cry, now you get it, obviously. I will explain what this means properly later on in this post. But first I will state what it means. If true it implies a lot of things about the distribution of prime numbers, and as you may or may not know they are very irregular and very difficult to find as the numbers get very, very big.
To track back to my earlier point, what is the Riemann Zeta Function ( it is denoted as ζ(s), ζ being the Greek lower case from which z was derived)?
This requires that you understand sequences and series, imaginary numbers and imaginary exponents. The real intrigue of this comes from the fact that it can be represented by Euler's product.
As you may or may not notice this is comprised of the prime numbers, this means that there is a sort of subliminal link between the natural numbers and the prime numbers. This showed that the prime numbers were not just positioned randomly and are not merely the building blocks to numbers but there is an actual link between them and the natural numbers.
The Riemann Zeta Function on its face doesn't look too difficult, I mean it is just an infinite sequence, even with a complex power you'd expect this to be possible and even pretty easy. But that is not the case at all, part of the reason is how sporadic complex exponents can be, and although it is not too difficult to find solutions (using a high powered computer thousands can be found each hour) it is incredibly, incredibly hard to find a proof for all the solutions.
You can see, this function seems to have little to no consistency to it, but a fair amount is known about the function. A lot of the zeros do actually satisfy the hypothesis, over 10 trillion of them in fact. And you'd think that is a proof alone, but as it often involves an iterated log (a log of a log, log(log(x)) and this increases very, very, very slowly in fact log(log(10,000,000,000)) = 1, so 10 trillion really isn't anything. If it is still holding true for log(log(x))>40 there may be a greater unanimous opinion on the truth of the hypothesis.
Every mathematician worth his salt has had an encounter with the Riemann Hypothesis and it has withheld every single attempt thus far. The maths used to try and tackle the problem is so complex that entirely new branches of mathematics have been created to deal with it, this maths to laymen has literally nothing, at all, to do with the prime numbers. It is so complex and far away from the problem that it almost boggles mathematicians minds, but it consumes them, it is their passion and life.
Prime numbers are the passion for many and the Riemann Hypothesis is merely an extension of that, and hopefully it will be solved in my life time.
If you have caught the prime number bug I suggest you read the excellent book by Karl Sabbagh called Dr Riemann's Zeros.
But what actually is the Riemann Hypothesis? It is a conjecture about the location of the non-trivial zeros of the Riemann Zeta function, it states that all the zeros should lie on the critical strip 0.5+it. "Oh yeah!", I hear you cry, now you get it, obviously. I will explain what this means properly later on in this post. But first I will state what it means. If true it implies a lot of things about the distribution of prime numbers, and as you may or may not know they are very irregular and very difficult to find as the numbers get very, very big.
To track back to my earlier point, what is the Riemann Zeta Function ( it is denoted as ζ(s), ζ being the Greek lower case from which z was derived)?
 |
| Where s is an imaginary number, a+ib. |
As you may or may not notice this is comprised of the prime numbers, this means that there is a sort of subliminal link between the natural numbers and the prime numbers. This showed that the prime numbers were not just positioned randomly and are not merely the building blocks to numbers but there is an actual link between them and the natural numbers.
The Riemann Zeta Function on its face doesn't look too difficult, I mean it is just an infinite sequence, even with a complex power you'd expect this to be possible and even pretty easy. But that is not the case at all, part of the reason is how sporadic complex exponents can be, and although it is not too difficult to find solutions (using a high powered computer thousands can be found each hour) it is incredibly, incredibly hard to find a proof for all the solutions.
 |
| The plot of the Riemann Zeta Function, the red line is the real part, the blue part is the imaginary part. |
Every mathematician worth his salt has had an encounter with the Riemann Hypothesis and it has withheld every single attempt thus far. The maths used to try and tackle the problem is so complex that entirely new branches of mathematics have been created to deal with it, this maths to laymen has literally nothing, at all, to do with the prime numbers. It is so complex and far away from the problem that it almost boggles mathematicians minds, but it consumes them, it is their passion and life.
Prime numbers are the passion for many and the Riemann Hypothesis is merely an extension of that, and hopefully it will be solved in my life time.
If you have caught the prime number bug I suggest you read the excellent book by Karl Sabbagh called Dr Riemann's Zeros.
Labels:
amazing,
beauty,
imaginary numbers,
logs,
maths is fun,
Prime numbers,
riemann hypothesis
Thursday, 24 November 2011
Maths and the Real World: Bayes' Theorem
Bayes' Theorem is one of the most practical theorems to apply to everyday life and if used correctly it can be an indispensable decision making tool. In a nutshell what the Bayes' Theorem does is measure the confidence that something is true. It takes the uncertainty before and after observing the modelled system and links the two.
We shall use an example to help explain what the Bayes' Theorem is and how it works. Let's consider the example that you have had a persistent headache for a week now and you're not certain what the cause it. But you do believe that it is caused either by stress (hypothesis A) or by having caffeine (hypothesis B).
So to test if stress is the key to the chronic headaches you have a day of relaxation whilst you've got a headache and have had coffee on the same day. By the end your headache has gone, so this can be considered as evidence. This should have some relation to how much more likely is A than B. But how strong is this evidence exactly? And how do we show which hypothesis it supports? Bayes' Theorem tells us that these answers lie in what is called the Bayes' Factor.
The Bayes' Factor is the question: "How much more likely would it be for this evidence to occur if A were true than if B were true?". This question must lead to one of three conclusions:
We shall use an example to help explain what the Bayes' Theorem is and how it works. Let's consider the example that you have had a persistent headache for a week now and you're not certain what the cause it. But you do believe that it is caused either by stress (hypothesis A) or by having caffeine (hypothesis B).
So to test if stress is the key to the chronic headaches you have a day of relaxation whilst you've got a headache and have had coffee on the same day. By the end your headache has gone, so this can be considered as evidence. This should have some relation to how much more likely is A than B. But how strong is this evidence exactly? And how do we show which hypothesis it supports? Bayes' Theorem tells us that these answers lie in what is called the Bayes' Factor.
The Bayes' Factor is the question: "How much more likely would it be for this evidence to occur if A were true than if B were true?". This question must lead to one of three conclusions:
- The evidence would be more likely to occur if A were true than if B were true. This means that the evidence supports A rather than B.
- The evidence would be just as likely to occur if A or B were true. This means that the evidence has no real weight to whether A or B is more likely to be correct. That means that the "evidence" is not actually evidence at all.
- The evidence would be more likely to occur if B were true than if A were true. This means that the evidence supports B rather than A.
In our example of chronic headaches the Bayes' factor becomes: "How much more likely would it be for the headache to disappear after having a day of relaxation if stress were the cause compared to if caffeine was the cause?".
Now we do do not know the precise answer to this, but we can give a rough approximation to it. A day of relaxation could have some effect at stopping a headache if caffeine was the cause, but it shouldn't have too much of an effect, no more than a 1 in 5 chance for a persistent headache. On the other hand if the factor of stress is dealt with and the headache disappears, that is a pretty good indication that stress is the key cause, so the chances that stress is the main cause is about 1 in 2.
How likely the headache would have stopped given A is 1/2. How likely the headache would have stopped given B is 1/5. Hence the Bayes' factor, how likely would it be for the headache to stop given A compared to how likely it was to stop given B, is at least (1/2) / (1/5) = 2.5.
This means that given our evidence we should now believe that A is at least 2.5 times more likely compared to B, this is compared to what we used to think. The Bayes' factor tells us how much more our new evidence should cause us to believe the likelihood of one of our hypotheses.
Now let's suppose that you already suspected that stress was twice as likely to be the main cause (as you had recently taken on more responsibility causing more stress). Now we know that the Bayes' Factor is at that A is at least 2.5 times more likely than B, but as we already believe A to be twice as likely as B we know that A is now at least 5 times more likely than B.
Bayes' Theorem is useful because it tells us the correct sort of question to ask ourselves and then it uses maths and statistics to provide us with a suitable answer and easy to understand conclusion. Bayes' Theorem can also provide an answer when looking at just one variable, you simply change B to to A' (not A).
However as humans we tend to have a very poor ability at distinguishing what is or isn't evidence. If we're expecting a particular result we're far more likely to apply whatever evidence we've got and assess it with bias.
So the important part of interpreting the evidence we now have is to always use the question "How much more likely would it be for this evidence to occur if A were true than if B were true?". In the next post I do I will be writing about the maths behind Bayes' theorem.
Now we do do not know the precise answer to this, but we can give a rough approximation to it. A day of relaxation could have some effect at stopping a headache if caffeine was the cause, but it shouldn't have too much of an effect, no more than a 1 in 5 chance for a persistent headache. On the other hand if the factor of stress is dealt with and the headache disappears, that is a pretty good indication that stress is the key cause, so the chances that stress is the main cause is about 1 in 2.
How likely the headache would have stopped given A is 1/2. How likely the headache would have stopped given B is 1/5. Hence the Bayes' factor, how likely would it be for the headache to stop given A compared to how likely it was to stop given B, is at least (1/2) / (1/5) = 2.5.
This means that given our evidence we should now believe that A is at least 2.5 times more likely compared to B, this is compared to what we used to think. The Bayes' factor tells us how much more our new evidence should cause us to believe the likelihood of one of our hypotheses.
Now let's suppose that you already suspected that stress was twice as likely to be the main cause (as you had recently taken on more responsibility causing more stress). Now we know that the Bayes' Factor is at that A is at least 2.5 times more likely than B, but as we already believe A to be twice as likely as B we know that A is now at least 5 times more likely than B.
Bayes' Theorem is useful because it tells us the correct sort of question to ask ourselves and then it uses maths and statistics to provide us with a suitable answer and easy to understand conclusion. Bayes' Theorem can also provide an answer when looking at just one variable, you simply change B to to A' (not A).
However as humans we tend to have a very poor ability at distinguishing what is or isn't evidence. If we're expecting a particular result we're far more likely to apply whatever evidence we've got and assess it with bias.
So the important part of interpreting the evidence we now have is to always use the question "How much more likely would it be for this evidence to occur if A were true than if B were true?". In the next post I do I will be writing about the maths behind Bayes' theorem.
Labels:
amazing,
bayes,
interesting,
maths,
nerdy,
real world
Monday, 31 October 2011
Different Sizes of Infinity
Before you read this make sure you have a basic knowledge of sets.
The "cardinality" of something is the size of a set. For example the cardinality of the set {3, 2, 17, -9} is 4, and the cardinality of the set {2, 6, -7} is 3. But when thinking it terms of infinity things become more confusing, I mean how can you categorise different sizes of infinity, infinity surely must just be infinity, right?
Well unfortunately, no. Using the ideas of sets we can find that there are actually different cardinalities of infinity. But to find this we need a more general definition of what being the "same sized set" is. A set {1, 2, 3, ..., x-1, x} has a cardinality of x and the set {1, 2, 3, ..., y-1, y} has a cardinality of y, the sets will be the same size if x = y. This then leads to the definition that being the "same size" is if the sets have the same amount of elements.
When we check if a set is the same size as another set, we simply count the number of elements in both sets and compare. But with infinite sets this is (obviously), impossible. But if we break the task down a bit we find ways of managing this. Take the elements from each set and pair them up, if they do match up perfectly with no doubling up or ignoring any elements then the sets are the same size.
Now if we pair the natural numbers, N {1, 2, 3, ...}, and the integers, Z {-2, -1, 0, 1, 2, ...}, we will be able to see which set is larger. We pair the numbers up like so:
And you can see, that despite your better knowledge, the numbers are pairing up and will continue to do perfectly infinitely. This then means that the sets of both the natural numbers and integers are the same size and thus have the same cardinality. This cardinality is referred to as: ℵ0 (read as "aleph null" or "aleph zero"). The aleph, "ℵ", character is used as it is the first letter in the Hebrew word 'infinity'. ℵ0 refers to 'countable infinity', or in simpler terms the lowest possible form of infinity.
When we continue to pair up the numbers we discover that the rational numbers and the natural numbers are too the exact same size and thus the cardinality of the rational numbers is also ℵ0. In fact the prime numbers are also deemed to have the same cardinality as the natural numbers, integers and rational numbers. I know it seems insane, but it is true.
And going back to my earlier point there are larger cardinalities of infinity. As you would think the next cardinality of infinity is ℵ1. The size of the real numbers in fact are larger that the natural numbers, integers, etc., this is because the real numbers (in now way at all) can be paired to the natural numbers. Because, between 0 and 1 there an infinite number of real values that are there, in fact the same can be said between 0 and 0.000000001. Thinking of it in this way helps to visualise the fact that the set of real numbers must be larger than the set of natural numbers.
As far as ℵx goes it will exist as long as x is a natural number, but as x goes past 1 it becomes much harder to visualise how this infinity is larger than the last. But there can not be ℵ1.5 for example, this is the continuum hypothesis.
The "cardinality" of something is the size of a set. For example the cardinality of the set {3, 2, 17, -9} is 4, and the cardinality of the set {2, 6, -7} is 3. But when thinking it terms of infinity things become more confusing, I mean how can you categorise different sizes of infinity, infinity surely must just be infinity, right?
Well unfortunately, no. Using the ideas of sets we can find that there are actually different cardinalities of infinity. But to find this we need a more general definition of what being the "same sized set" is. A set {1, 2, 3, ..., x-1, x} has a cardinality of x and the set {1, 2, 3, ..., y-1, y} has a cardinality of y, the sets will be the same size if x = y. This then leads to the definition that being the "same size" is if the sets have the same amount of elements.
When we check if a set is the same size as another set, we simply count the number of elements in both sets and compare. But with infinite sets this is (obviously), impossible. But if we break the task down a bit we find ways of managing this. Take the elements from each set and pair them up, if they do match up perfectly with no doubling up or ignoring any elements then the sets are the same size.
Now if we pair the natural numbers, N {1, 2, 3, ...}, and the integers, Z {-2, -1, 0, 1, 2, ...}, we will be able to see which set is larger. We pair the numbers up like so:
And you can see, that despite your better knowledge, the numbers are pairing up and will continue to do perfectly infinitely. This then means that the sets of both the natural numbers and integers are the same size and thus have the same cardinality. This cardinality is referred to as: ℵ0 (read as "aleph null" or "aleph zero"). The aleph, "ℵ", character is used as it is the first letter in the Hebrew word 'infinity'. ℵ0 refers to 'countable infinity', or in simpler terms the lowest possible form of infinity.
When we continue to pair up the numbers we discover that the rational numbers and the natural numbers are too the exact same size and thus the cardinality of the rational numbers is also ℵ0. In fact the prime numbers are also deemed to have the same cardinality as the natural numbers, integers and rational numbers. I know it seems insane, but it is true.
And going back to my earlier point there are larger cardinalities of infinity. As you would think the next cardinality of infinity is ℵ1. The size of the real numbers in fact are larger that the natural numbers, integers, etc., this is because the real numbers (in now way at all) can be paired to the natural numbers. Because, between 0 and 1 there an infinite number of real values that are there, in fact the same can be said between 0 and 0.000000001. Thinking of it in this way helps to visualise the fact that the set of real numbers must be larger than the set of natural numbers.
As far as ℵx goes it will exist as long as x is a natural number, but as x goes past 1 it becomes much harder to visualise how this infinity is larger than the last. But there can not be ℵ1.5 for example, this is the continuum hypothesis.
Labels:
aleph,
amazing,
beauty,
cardinality,
infinity,
insane,
intelligent,
maths,
mind boggling,
numbers,
sets,
statistics
Thursday, 6 October 2011
Squaring Numbers Under 100
First, I must state that although you do not necessarily require any prior knowledge other than to be competent at maths, it does not hurt if you know the square numbers up to 10 and are reasonably good at quadratic equations.
I recently discovered this technique of timesing numbers together recently and I was pretty proud of myself and have been using to bamboozle my friends and family. However I did not create this technique, I do not know who did, but if you do please leave a comment.
I am starting by squaring a number, as the skills learnt from that will help you when you times two different numbers together, which I will cover in a later blog post.
To begin with when squaring a number we need to choose one number as a base, we will call it 'a', for example if we had 43 our base would be 40. If we had 47 however I would personally choose 50, as dealing with 3 is easier than dealing with 7. This second number we will call, 'n', to get 'n' you take the base from the original number, 'o'.
n = o-a
You may see where we are going here, we will take the equation (a+n) and square it, that is all we have to do. The product of this will be a²+2an+n². So for example if we wanted to find the answer to 76²:
a = 80, n = 76-80 = -4
80²+2(80*-4)+(-4)²
6400-640+16 = 5776
After a little bit of practice you can do this very efficiently and very quickly in your head.
I recently discovered this technique of timesing numbers together recently and I was pretty proud of myself and have been using to bamboozle my friends and family. However I did not create this technique, I do not know who did, but if you do please leave a comment.
I am starting by squaring a number, as the skills learnt from that will help you when you times two different numbers together, which I will cover in a later blog post.
To begin with when squaring a number we need to choose one number as a base, we will call it 'a', for example if we had 43 our base would be 40. If we had 47 however I would personally choose 50, as dealing with 3 is easier than dealing with 7. This second number we will call, 'n', to get 'n' you take the base from the original number, 'o'.
n = o-a
You may see where we are going here, we will take the equation (a+n) and square it, that is all we have to do. The product of this will be a²+2an+n². So for example if we wanted to find the answer to 76²:
a = 80, n = 76-80 = -4
80²+2(80*-4)+(-4)²
6400-640+16 = 5776
After a little bit of practice you can do this very efficiently and very quickly in your head.
Labels:
amazing,
interesting,
large numbers,
maths,
squaring numbers
Tuesday, 29 March 2011
Imaginary Numbers
When you first begin studying mathematics you are taught that only positive numbers can be square rooted, and this is true for conventional mathematics and it is not too often that you need to square root a negative number; but what if it does arise? How would that even happen?
Well, usually you never really need to square root a negative number. But when plotting quadratic graphs it is always a possibility that the square root of a negative may come up.
You may remember that if b²-4ac < 0 then the quadratic has no real roots, emphasis on the word no real roots. A quadratic equation will always have roots, just imaginary numbers will be involved if b²-4ac < 0.
But what is an imaginary number? It is denoted by the character i and this is representative of √-1. Like all square roots, √-1 has two answers, ±i.
So say, for example we had a quadratic equation where b²-4ac < 0. We could, in fact, solve it. If we had a quadratic equation, 3x²+8x+11=0 we could solve this by completing the square or using the formula, I prefer to complete the square but you would get the same outcome regardless:
Okay, it allows you to discover solutions to previously impossible quadratics, big woop? Well, imaginary numbers are in fact incredibly important! The Schrödinger Equation (the fundamental equation in quantum mechanics) using imaginary numbers.
Well, usually you never really need to square root a negative number. But when plotting quadratic graphs it is always a possibility that the square root of a negative may come up.
You may remember that if b²-4ac < 0 then the quadratic has no real roots, emphasis on the word no real roots. A quadratic equation will always have roots, just imaginary numbers will be involved if b²-4ac < 0.
But what is an imaginary number? It is denoted by the character i and this is representative of √-1. Like all square roots, √-1 has two answers, ±i.
So say, for example we had a quadratic equation where b²-4ac < 0. We could, in fact, solve it. If we had a quadratic equation, 3x²+8x+11=0 we could solve this by completing the square or using the formula, I prefer to complete the square but you would get the same outcome regardless:
|
|
| If you do not understand this, do not panic! Simply submit a comment and I will respond, explaining how to do this using other methods. |
| The Schrodinger Equation |
Engineers also using imaginary numbers as a way to view "phase", this is however denoted by 'j' as 'I' is used for current. Potential energy is also necessary to be seen when carrying out these calculations, this creates a complex number in the form, a+bi, where 'a' and 'b' are integers and 'i' (or 'j'!) is an imaginary number.
But how are complex numbers represented? They are represented as numbers on a complex plane, with the x-axis being the real axis and the y-axis being the imaginary axis. It is rare that you would find an imaginary number used on its own, it will often be in partnership with another, regular number, as a complex number.
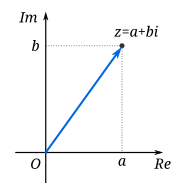 |
| The representation of a complex number on a complex plane. |
Imaginary Number Facts:
- You can in fact do xi, it isn't the easiest thing to do, but it is perfectly possible and you will be able to it after a little bit of practice, for the whole breakdown on why please visit my newer blog post: imaginary exponents.
- Another noteworthy idea is that an imaginary number can also be square rooted! These are roughly (0.707106+0.707106i) and (-0.707106-0.707106i), or as a fraction (1/√2)(1/i) and (-1/√2)(1/i). Try to square them, you will see it works.
- Imaginary numbers follow a pattern when put to differing powers, this pattern goes: 1, i, -1, -i. You can find out what ix is simply by checking what the remainder is when x is divided by 4. If the remainder is equal to 0 then it will equal i. If it has a remainder of 1 then the answer will be 1, remainder 2 will equal -1 and finally a remainder of 3 will be -i.
Labels:
amazing,
complex,
engineering,
imaginary numbers,
intelligent,
maths,
quantum mechanics,
science,
technology
Monday, 28 March 2011
Maths and the Real World
"Go deep down into anything and you will find mathematics" - Dean Schlicter
Often a lot of students who first begin algebra or quadratic equations fail to see how this has any implications on the real world. The aim of secondary school seems less to inform about the uses and necessities of mathematics and more on driving the knowledge into your head.
But maths in all its bewildering complexity and brute simplicity is all around us whether we choose to acknowledge it or not. Science is all compromised from formulas and predictions, all of which is algebra. Some of the greatest and most eloquent works in science are equations.
The basis of quantum mechanics, the Schrödinger Equation, is a relatively complex form of algebra involving constants and variables to plot possible points at which a particle can be at. Almost the entirety of mechanics relies on inputting numbers to calculate forces and other movements. And engineering is virtually completely maths. The importance of algebra is clear for all to know.
Bertrand Russell famously said that: "Mathematics, rightly viewed, possesses not only truth, but supreme beauty". And the majesty that maths holds can be represented by the elegance of space. Space is perhaps one of the only ways to think of infinity, the size of which we can currently see is 46 billion years, or around 45,000,000,000,000,000,000,000,000 kilometres in radius. Estimates of planet sizes, dark matter and even black holes; all are only possible with maths and how it is implied to the real world and the universe.
Nature also likes to throw in a little bit of maths occasionally, times of the year when animals hibernate and mate are often prime years as they're harder to predict because of a lack of a pattern. The fibonacci spiral is seen in many natural phenomena, as well as perfect shapes occurring regularly.
I will also do a future post discussing the economy, how it works and how maths is applied to that.
Often a lot of students who first begin algebra or quadratic equations fail to see how this has any implications on the real world. The aim of secondary school seems less to inform about the uses and necessities of mathematics and more on driving the knowledge into your head.
But maths in all its bewildering complexity and brute simplicity is all around us whether we choose to acknowledge it or not. Science is all compromised from formulas and predictions, all of which is algebra. Some of the greatest and most eloquent works in science are equations.
The basis of quantum mechanics, the Schrödinger Equation, is a relatively complex form of algebra involving constants and variables to plot possible points at which a particle can be at. Almost the entirety of mechanics relies on inputting numbers to calculate forces and other movements. And engineering is virtually completely maths. The importance of algebra is clear for all to know.
.
However, my love for maths does not come from number crunching. Altering one number into another via some function, is of course the most obvious way in which maths is related to everything, but it is not the beautiful way.Bertrand Russell famously said that: "Mathematics, rightly viewed, possesses not only truth, but supreme beauty". And the majesty that maths holds can be represented by the elegance of space. Space is perhaps one of the only ways to think of infinity, the size of which we can currently see is 46 billion years, or around 45,000,000,000,000,000,000,000,000 kilometres in radius. Estimates of planet sizes, dark matter and even black holes; all are only possible with maths and how it is implied to the real world and the universe.
.
Labels:
amazing,
infinity,
interesting,
maths,
real world,
science,
universe
Wednesday, 16 March 2011
Now, undoubtedly you would have heard of Google, in fact there's a high chance you use Google for the majority of your daily activities on the web. They own: Google Mail (duh!), YouTube and Google Documents. These are enough to maintain the average users internet usage in a day.
Google has to deal with upwards of 7 billion hits every, single day and that equates to 20 petabytes of data processed everyday. How big is a petabyte? Over one million gigabytes. 50 petabytes would cover the entire written works of mankind in recorded history, in all languages. That should give you a brief glimpse into the enormity that is Google.
A company that in 2009 made over $6,000,000,000 in profit. A company that allows its employees to have 20% of its working day to be used to work on projects they enjoy. It's proved to be a rather resounding success with newer services such as Google Mail, Google News, Orkut and AdSense originating from the 20% of "free time". The most successful internet business in the world and it's amazing to it's employees, that is surely a business model that all companies should adopt.
But none of this compares to their business plan, it really is amazing. They make around 99% of their revenue from advertising in the many forms that they offer it. So it would obviously make sense to encourage people to visit places where their adverts are present.
Now what businesses have Google recently bought into and began focusing their attentions on? Double Click, Android, Google Docs, AdMob and Google Chrome OS. This is just a minute portion of the 90+ companies they have acquired in the last ten years and in recent times has increased rapidly, with 4 companies bought this month (just a fortnight in!).
The biggest acquisition to date was that of Double Click, an advertising application. AdMob, advertising. And the rest encourage cloud computing, driving more visitors online and to Google's products and advertising. This creates greater revenue, and means any competition that Google has needs to constantly improve it's product, whatever happens though people are drove onto the internet and thus they gain revenue. Ingenius.
Google has to deal with upwards of 7 billion hits every, single day and that equates to 20 petabytes of data processed everyday. How big is a petabyte? Over one million gigabytes. 50 petabytes would cover the entire written works of mankind in recorded history, in all languages. That should give you a brief glimpse into the enormity that is Google.
A company that in 2009 made over $6,000,000,000 in profit. A company that allows its employees to have 20% of its working day to be used to work on projects they enjoy. It's proved to be a rather resounding success with newer services such as Google Mail, Google News, Orkut and AdSense originating from the 20% of "free time". The most successful internet business in the world and it's amazing to it's employees, that is surely a business model that all companies should adopt.
But none of this compares to their business plan, it really is amazing. They make around 99% of their revenue from advertising in the many forms that they offer it. So it would obviously make sense to encourage people to visit places where their adverts are present.
Now what businesses have Google recently bought into and began focusing their attentions on? Double Click, Android, Google Docs, AdMob and Google Chrome OS. This is just a minute portion of the 90+ companies they have acquired in the last ten years and in recent times has increased rapidly, with 4 companies bought this month (just a fortnight in!).
The biggest acquisition to date was that of Double Click, an advertising application. AdMob, advertising. And the rest encourage cloud computing, driving more visitors online and to Google's products and advertising. This creates greater revenue, and means any competition that Google has needs to constantly improve it's product, whatever happens though people are drove onto the internet and thus they gain revenue. Ingenius.
Labels:
adverts,
amazing,
brilliant,
google,
interesting,
Miscellaneous,
profit,
revenue
Sunday, 13 March 2011
Googol
No, my title is not a spelling error of Google. Googol is a number, a big number, a number that was so large and intriguing it inspired two nerdy University Student to create an easily available to everyone search engine to bring all of the internet to anyone. But talking about Google being awesome is a different article for a different time.
In this article I'm going to discuss the number a googol and a googolplex. Firstly what are they? Well a googol is 10100, that is a one followed by one hundred zeros, or the less catchy title, ten duotrigintillion. Just how big is that then? Well, there is estimated to be about 1.33×1050 atoms in the entire Earth. A googol is almost 1050 as much as this number. Nothing like maths to make you feel tiny and insignificant.
If you think that's large, your head may just explode when you're introduce to a googolplex. A googolplex is 10googol, that is enormous. A one followed by a googol zeros. That is so large it is almost impossible to comprehend. I'll try my best to explain just how mammothly big this number is.
Astronomer Carl Sagan estimated that writing a googolplex would be impossible, why? It would require more space than the known universe can provide. Seriously. There is only about 2.5×1089 elementary particles in the known universe, so even if every particle was a digit, it would still need the observable universe to be about one hundred billion times larger.
But, if you could fit the number into the known universe it would take an unbelievable amount of time to write. If you could write 120 digits a minute, it would take around 1.51×1092 years to finish (almost a googolplex years!). This amount of time is 1082 times the age of the universe. So, I wouldn't really start trying to write it out. There's a high chance, that even if it was possible to write for that period of time, that the entire universe will have inevitably died.
A more nerdy way to try and explain the size of a googolplex is to look at Planck time. Planck time (which I won't go into too much detail now), is the time it takes for light to travel one Planck length in a vaccuum, which is roughly 5.4×10-44, this is unbelievably quick. A googol is larger than the estimated amount of Planck times that have past since the start of the universe (8×1060), so a googolplex is much, much larger than even the smallest measurement of time that has past since the dawn of everything.
There is however a larger number that still has a use, it is known as Graham's number. But that's a different article for a different time. I hope this post has given you a small idea into the enormity Maths can hold.
In this article I'm going to discuss the number a googol and a googolplex. Firstly what are they? Well a googol is 10100, that is a one followed by one hundred zeros, or the less catchy title, ten duotrigintillion. Just how big is that then? Well, there is estimated to be about 1.33×1050 atoms in the entire Earth. A googol is almost 1050 as much as this number. Nothing like maths to make you feel tiny and insignificant.
If you think that's large, your head may just explode when you're introduce to a googolplex. A googolplex is 10googol, that is enormous. A one followed by a googol zeros. That is so large it is almost impossible to comprehend. I'll try my best to explain just how mammothly big this number is.
Astronomer Carl Sagan estimated that writing a googolplex would be impossible, why? It would require more space than the known universe can provide. Seriously. There is only about 2.5×1089 elementary particles in the known universe, so even if every particle was a digit, it would still need the observable universe to be about one hundred billion times larger.
But, if you could fit the number into the known universe it would take an unbelievable amount of time to write. If you could write 120 digits a minute, it would take around 1.51×1092 years to finish (almost a googolplex years!). This amount of time is 1082 times the age of the universe. So, I wouldn't really start trying to write it out. There's a high chance, that even if it was possible to write for that period of time, that the entire universe will have inevitably died.
A more nerdy way to try and explain the size of a googolplex is to look at Planck time. Planck time (which I won't go into too much detail now), is the time it takes for light to travel one Planck length in a vaccuum, which is roughly 5.4×10-44, this is unbelievably quick. A googol is larger than the estimated amount of Planck times that have past since the start of the universe (8×1060), so a googolplex is much, much larger than even the smallest measurement of time that has past since the dawn of everything.
There is however a larger number that still has a use, it is known as Graham's number. But that's a different article for a different time. I hope this post has given you a small idea into the enormity Maths can hold.
Labels:
amazing,
enormous,
googol,
googolplex,
graham's number,
huge,
maths,
numbers
Monday, 28 February 2011
Pi
Pi (π), Mathematicians are engulfed by it and for good reason. It really is the definition of 'Eloquent Math'; an irrational number that is one of the most important constants used in Mathematics that can be so simply found and represented. Circumference of a circle/diameter of circle.
Pi is a number, which for a lack of better words is a number that is infinite and does not repeat its decimal representation at any stage; this alone makes it rather unique (barring Euler's constant and √2) and perhaps that is a reason behind it having such a huge popularity amongst Mathematicians and nerds alike.
At the current moment in time pi has been calculated to over one trillion decimal places, that my friends is how fixated Mathematicians are on pi! However this is really not necessary other than pure curiousity and looking for patterns in pi and to try and understand it some more. Pi calculated to 11 decimal places can accurately estimate the circumference of any circle that fits inside of the Earth to one millimetre; and if pi is represented to 39 decimal places you can estimate the circumference of any circle inside the observable universe to the radius of one hydrogen atom. To a trillion decimal places there would be nie on zero error whatsoever (about 3*10^-10 the radius of a hydrogen atom).
If you are beginning to be as fascinated with pi as I, and many others are, take a look around the internet and at the link to Yann Martel's "Life of Pi " that is a very compelling read.
" that is a very compelling read.
Or if you'd prefer, the hardcover:



Pi is a number, which for a lack of better words is a number that is infinite and does not repeat its decimal representation at any stage; this alone makes it rather unique (barring Euler's constant and √2) and perhaps that is a reason behind it having such a huge popularity amongst Mathematicians and nerds alike.
At the current moment in time pi has been calculated to over one trillion decimal places, that my friends is how fixated Mathematicians are on pi! However this is really not necessary other than pure curiousity and looking for patterns in pi and to try and understand it some more. Pi calculated to 11 decimal places can accurately estimate the circumference of any circle that fits inside of the Earth to one millimetre; and if pi is represented to 39 decimal places you can estimate the circumference of any circle inside the observable universe to the radius of one hydrogen atom. To a trillion decimal places there would be nie on zero error whatsoever (about 3*10^-10 the radius of a hydrogen atom).
If you are beginning to be as fascinated with pi as I, and many others are, take a look around the internet and at the link to Yann Martel's "Life of Pi
Or if you'd prefer, the hardcover:

Labels:
amazing,
amazon,
irrational,
maths,
pi
Subscribe to:
Posts (Atom)

+mod+m.png)
+mod+m.png)








