Imaginary Numbers

When you first begin studying mathematics you are taught that only positive numbers can be square rooted, and this is true for conventional mathematics and it is not too often that you need to square root a negative number; but what if it does arise? How would that even happen?


Well, usually you never really need to square root a negative number. But when plotting quadratic graphs it is always a possibility that the square root of a negative may come up.


You may remember that if b²-4ac < 0 then the quadratic has no real roots, emphasis on the word no real roots. A quadratic equation will always have roots, just imaginary numbers will be involved if b²-4ac < 0.


But what is an imaginary number? It is denoted by the character i and this is representative of √-1. Like all square roots, √-1 has two answers, ±i.


So say, for example we had a quadratic equation where b²-4ac < 0. We could, in fact, solve it. If we had a quadratic equation, 3x²+8x+11=0 we could solve this by completing the square or using the formula, I prefer to complete the square but you would get the same outcome regardless:

If you do not understand this, do not panic! Simply submit a
comment and I will respond, explaining how to do this using
other methods.

Okay, it allows you to discover solutions to previously impossible quadratics, big woop? Well, imaginary numbers are in fact incredibly important! The Schrödinger Equation (the fundamental equation in quantum mechanics) using imaginary numbers. 

The Schrodinger Equation

Engineers also using imaginary numbers as a way to view "phase", this is however denoted by 'j' as 'I' is used for current. Potential energy is also necessary to be seen when carrying out these calculations, this creates a complex number in the form, a+bi, where 'a' and 'b' are integers and 'i' (or 'j'!) is an imaginary number.

But how are complex numbers represented? They are represented as numbers on a complex plane, with the x-axis being the real axis and the y-axis being the imaginary axis. It is rare that you would find an imaginary number used on its own, it will often be in partnership with another, regular number, as a complex number.

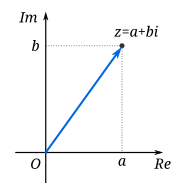The representation of a complex
 number on a complex plane.

Imaginary Number Facts:

• You can in fact do xⁱ, it isn't the easiest thing to do, but it is perfectly possible and you will be able to it after a little bit of practice, for the whole breakdown on why please visit my newer blog post: imaginary exponents.
• Another noteworthy idea is that an imaginary number can also be square rooted! These are roughly (0.707106+0.707106i) and (-0.707106-0.707106i), or as a fraction (1/√2)(1/i) and (-1/√2)(1/i). Try to square them, you will see it works.
• Imaginary numbers follow a pattern when put to differing powers, this pattern goes: 1, i, -1, -i. You can find out what i^x is simply by checking what the remainder is when x is divided by 4. If the remainder is equal to 0 then it will equal i. If it has a remainder of 1 then the answer will be 1, remainder 2 will equal -1 and finally a remainder of 3 will be -i.