Fibonacci Numbers and Continued Fractions

I feel I needed an updated post on the Fibonacci sequence with some of the more core ideas behind it, you can still access the old post.

The definition of the Fibonacci sequence is:

$\begin{align}F_{n+2}=F_{n+1}=F_n\ where\ F_0=1,\ F_1=1\end{align}$

You can see quickly that the first few values of the sequence are 1, 1, 2, 3, 5, 8, 13, ..., etc. this is a weakly increasing sequence, that is ${F}_{n+1}\ge F_n \forall\ n \ge 1$.

This clearly means that the sequence does not tend towards a limit, but does the ratio between terms tend towards a limit?

Consider that the $\lim_{n\to\infty}(\frac{F_{n+1}}{F_n})=x$. If we divide $(1)$ through by $F_{n+1}$ we get:

$\begin{align*}\frac{F_{n+2}}{F_{n+1}}=1 + \frac{F_n}{F_{n+1}}\end{align*}\tag{2}$

Clearly from our definition of the $\lim_{n\to\infty}(\frac{F_{n+1}}{F_n})=x$ we get that $(2)\equiv x=1+\frac{1}{x}$. This is easy enough to solve, we simply multiply through by $x$ and rearrange to get a quadratic we can solve.

$\begin{align*}x^2-x-1=0
\\\Rightarrow x = \frac{1\pm\sqrt{5}}{2}\end{align*}$

Only one of these two possible x values are logical, as the sequence is weakly increasing and all of the terms are greater than or equal to 0 clearly the ratio between terms is positive $\therefore\ x = \frac{1+\sqrt{5}}{2}$. This is the golden ratio, $\phi$.

Our definition that $x=1+\frac{1}{x}$ has interesting implications when we represent it as a recurrence relation, $x_{n+1}=1+\frac{1}{x_n}$. If we set $x_0 = 1$ then $x_1 = 1+\frac{1}{1},\ x_2 = 1 + \frac{1}{1+\frac{1}{1}}$, etc. This continues on such that $\lim_{n\to\infty}(x_{n+1})\equiv\phi = 1 + \frac{1}{1+\frac{1}{1+\frac{1}{\ddots}}}$, this is an example of an infinite continued fraction.

A continued fraction is essentially fractions within fractions (frac-cep-tions?), $a_1 + \frac{1}{a_2 + \frac{1}{\ddots \, + \frac{1}{a_m}}}$.

An infinite continued fraction is one that does not terminate after a finite sequence of iterations, $a_1 + \frac{1}{a_2 + \frac{1}{\ddots}}$. An irrational number can be continually, more accurately, approximated using infinite continued fractions.

If we want to represent any integers as an infinite continued fractions we can begin by thinking of the general continued fraction:

$\begin{align*}a=\frac{k}{1+\frac{k}{1+\frac{k}{\ddots}}} \Rightarrow a=\frac{k}{1+a} \Rightarrow a^2+a-k=0\end{align*}\tag{3}$

For a to be rational in this quadratic $1+4k$ must be a square number, clearly this square will be odd (odd + even = odd) from this you can quickly calculate the first few values of k to be $k = 2,\ 6,\ 12,\ 20,\ ...$, it can be quickly shown that the nth term $k_n=n^2+n$. Using the quadratic formula on $(3)$ we find that $a=\frac{-1+\sqrt{4(n^2+n)+1}}{2}\equiv\frac{-1\pm\sqrt{(2n+1)^2}}{2}\equiv\frac{2n}{2}=n$.

Therefore for all positive integers, a, we can represent them as an infinite continued fraction if and only if $k=a^2+a$. Or to put it mathematically:

$a=\frac{k}{1+\frac{k}{1+\frac{k}{\ddots}}},\ a\in\mathbb{N} \Leftrightarrow k=a^2+a$

This is one example of how useful (and fun!) continued fractions can be, they are also much more mathematically relevant than decimals as they provide a lot more useful information about the nature of the number itself.

See if you can express $\sqrt{2}$ as an infinite continued fraction. Leave any answers in the comment section.

Fibonacci Sequence

A sequence of integer numbers that after its first two numbers each subsequent term is the sum of the previous two terms: F_n=F_n-1+F_n-2

. The sequence is then of course infinite. The first 10 terms of the sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34

Now this in itself is not a very difficult or overly interesting/complex sequence. But the huge array of implications it has on the "real world" are incredibly interesting and in fact fascinating, if you're a nerd that is.

 

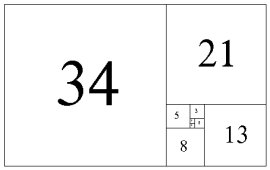
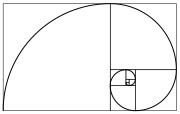
This is the Fibonacci tile, each square has the side length of what's in the middle of the square. Pretty but so what? Well, as all Mathematicians are, they weren't content with just turning a sequence into an array of squares and they looked deeper, don't they always? If you make a quarter circle from the tangents of each square and continue this way going through each square you end up with a spiral, obviously.

Oooh pretty, but big woop? Well yes, actually quite a massive big woop in fact. It is staggering how often either the Fibonacci spiral or sequence appears in nature. The branches of trees, arrangement of leaves, the flowering arrangements of certain flowers, the arrangement of a pine cone, the spiral of shells, the curvature of waves and even in family tree of bees, seriously. If you want to read about how the hell they're related please go here: http://en.wikipedia.org/wiki/Fibonacci_spiral#In_nature

Bees and the Fibonacci sequence, a match made in heaven. I'm waiting for my image to hit the papers, I'm pretty certain it will be voted the Scientific Breakthrough of the Year.

Other Random Facts:

Every positive integer can be wrote in a unique way as the of one or more Fibonacci terms and it will not include any two consecutive Fibonacci terms.

The Fibonacci Sequence can be used to determine tunings in music.

The Golden Ratio and Fibonacci Sequence are very, very closely related.