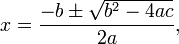If you have done Maths to a
secondary school level at some point you will have encountered circles, spheres
and pi. But this information may have passed over your head or you never really
went into the details of why these things work.
All circles have the amazing property that their circumference and
diameter are related by a ratio, this ratio is known as pi. The interesting
property about this number is that it is transcendental, this means that the
decimal expansion is non-repeating at any stage and continues on for infinity
(or in more formal mathematical terms, there is no polynomial with rational
coefficients where π is a root).
This property in itself is beautiful.
Pi has in fact been calculated to insane precision, to roughly ten trillion decimal places! This was obviously done using a computer, no human would try to take on this task (I sincerely hope). It is not very necessary to have such an accurate representation of π as if it is calculated to 11 decimal places you can accurately estimate the circumference of any circle that fits inside of the Earth to one millimetre. And if π is represented to 39 decimal places you can estimate the circumference of any circle inside the observable universe to the radius of one hydrogen atom. So 10 trillion decimal places is slightly unnecessary, but that is one way to get your name in the history books.
If you have ever really put any thought to maths you will often come to the thought of "why?". Why do the formulas we are told and have to recite work? And unfortunately, schools very rarely pay attention to the why and just have you use formulae blindly. And this thought is often the case with the area of a circle. We all know that it is πr2 but why is it that way? Like all maths that we use, it has been proved rigorously by many individuals.
Area of Circle:
Here is a rather simple proof of why the area of a circle is so. If we
split a circle into an even number of pieces we can rearrange them into a shape
that resembles a parallelogram.

All I have done with my circle of radius r is split it into 8 equal sectors and move them around so they interlock in a
parallelogram like shape. The top of the
parallelogram like object uses half of the chunks we have used, which is half of the circumference, which is πr. Again from GCSE Maths you may remember that the area of a
parallelogram is defined as base × height. As the sectors of the circle get smaller in width the parallelogram begins to take shape and the top and bottom of the shape begin to flatten out.
So sectors of width infinitely small will create a perfect parallelogram of height r and base πr, therefore the area of this parallelogram (and thus the circle) is πr2! And that is why we have our concise formula for the area of any circle.
There is also a proof for why a the volume of a sphere is also correct, but this requires some knowledge of calculus. So if you do not know calculus perhaps do not continue reading, however you are more than welcome to and then try to begin to understand calculus.
Volume of Sphere:
A sphere can be thought of as revolving a semi-circle around the x-axis. To do this consider a semi-circle circle with a centre at the origin and a radius of r, this will have an equation:
Any cross-section of the sphere derived by revolve the semi-circle, y, is a circle with a radius of y and an area of πy2! If we slice the sphere up into a infinite number of slices of infinitesimal thickness then the area of each slice is also it's volume (as it has an infinitely small thickness, essentially 0). So this means that the volume of each slice is πy2, if we add the volumes of every single slice then we get the total volume, which is that of a whole sphere!
This means that we are talking about integrating πy2 between r and -r to find the total area, and as area is the same as the volume for each slice the total volume.
And that's all! We have proved that formulae for the area of the circle and volume of a sphere are in fact correct. If there is anything at all that I have done here please do not hesitate to leave a comment and I will respond and explain to the best of my abilities.